题目内容
如图，直线AB、CD交于点A，∠ABC的平分线BD与∠ACB的平分线交于点O，与AC交于点D；过点O作EF∥BC交AB于E、交AC于F．若∠BOC=125°，若∠ABC：∠ACB=3：2，求∠AEF和∠EFC的度数．考点：等腰三角形的判定与性质,平行线的性质
专题：
分析：根据角平分线的定义可以求得∠ABC与∠ACB的度数，继而利用平行线的性质求得对应角的度数．
解答：解：∵∠ABC的平分线BD与∠ACB的平分线交于点O，
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
又∠BOC=125°，
∴∠OBC+∠OCB=180°-∠BOC=55°，
∴∠ABC+∠ACB=110°，
又∵∠ABC：∠ACB=3：2，
∴∠ABC=66°，∴∠ABC+∠ACB=44°，
∵EF∥BC，
∴∠AEF=∠ABC=66°，
∠AFE=∠ACB=44°，
∴∠EFC=180°-∠AFE=136°
∴∠AEF=66°，∠EFC=136°．
∴∠ABC=2∠OBC，∠ACB=2∠OCB，
又∠BOC=125°，
∴∠OBC+∠OCB=180°-∠BOC=55°，
∴∠ABC+∠ACB=110°，
又∵∠ABC：∠ACB=3：2，
∴∠ABC=66°，∴∠ABC+∠ACB=44°，
∵EF∥BC，
∴∠AEF=∠ABC=66°，
∠AFE=∠ACB=44°，
∴∠EFC=180°-∠AFE=136°
∴∠AEF=66°，∠EFC=136°．
点评：此题考查了三角形内角和定理和角平分线性质，特别注意此题中，∠BOC和∠A之间的关系：∠BOC=90°+
∠A．
| 1 |
| 2 |
练习册系列答案
字词句段篇系列答案
相关题目
下列分解因式错误的是（ ）
| A、y（x-y）+x（x-y）=（x-y）（x+y） |
| B、25x2-4y2=（5x+2y）（5x-2y） |
| C、4x2+20x+25=（2x+5）2 |
| D、a2（a-b）-2a（a-b）+b2（a-b）=（a-b）3 |
如图，已知⊙P和⊙O 相交于A、G两点，AB是⊙O的直径，且交⊙P于点E，⊙O的弦CD过点E，且CD⊥AB交⊙P于F，FA与⊙O交于M，且F、G、B三点在一条直线上，GE的延长线交⊙O于N，连结AN．
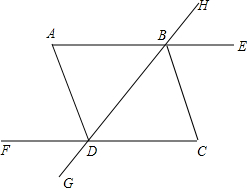如图，射线CF、AE被直线GH所截，交点分别为D、B，连结AD、CB，若∠HBE+∠GDC=180°，∠A=∠C，DA平分∠BDF．