题目内容
 如图,已知⊙P和⊙O 相交于A、G两点,AB是⊙O的直径,且交⊙P于点E,⊙O的弦CD过点E,且CD⊥AB交⊙P于F,FA与⊙O交于M,且F、G、B三点在一条直线上,GE的延长线交⊙O于N,连结AN.
如图,已知⊙P和⊙O 相交于A、G两点,AB是⊙O的直径,且交⊙P于点E,⊙O的弦CD过点E,且CD⊥AB交⊙P于F,FA与⊙O交于M,且F、G、B三点在一条直线上,GE的延长线交⊙O于N,连结AN.(1)求证:AB平分∠MAN;
(2)若N是
 |
| AB |
| 2 |
(3)若⊙O的半径为5,EF=2CE=6,求AN的长.
考点:圆的综合题
专题:综合题
分析:(1)根据圆周角定理得∠NAB=∠NGB,根据圆内接四边形的性质得∠NGB=∠FAE,则∠NAB=∠FAE,即AB平分∠MAN;
(2)连接ON,OM,如图1,由N是
的中点,根据垂径定理的推理得到NO⊥AB,则∠NAO=45°,所以∠FAE=45°,易判断△AOM为等腰直角三角形,根据等腰直角三角形的性质得OA=
AM;由于CD⊥AB,易得△AEF为等腰直角三角形,得到EF=AE,所以EF+BE=AB,加上AB=2OA,于是可得BE+EF=
AM;
(3)连接OC,BN,如图2,由EF=2CE=6得到CE=3,利用勾股定理,在Rt△OCE中计算出OE=4,则AE=9,在Rt△AEF中,再利用勾股定理计算出AF=3
,
由于AB为⊙O的直径,根据圆周角定理得∠ANB=90°,加上∠NAB=∠FAE,根据相似三角形的判定方法得到Rt△ANB∽Rt△AEF,然后利用相似比可计算出AN.
(2)连接ON,OM,如图1,由N是
 |
| AB |
| ||
| 2 |
| 2 |
(3)连接OC,BN,如图2,由EF=2CE=6得到CE=3,利用勾股定理,在Rt△OCE中计算出OE=4,则AE=9,在Rt△AEF中,再利用勾股定理计算出AF=3
| 13 |
由于AB为⊙O的直径,根据圆周角定理得∠ANB=90°,加上∠NAB=∠FAE,根据相似三角形的判定方法得到Rt△ANB∽Rt△AEF,然后利用相似比可计算出AN.
解答: (1)证明:∵∠NAB=∠NGB,
(1)证明:∵∠NAB=∠NGB,
而∠NGB=∠FAE,
∴∠NAB=∠FAE,
∴AB平分∠MAN;
(2)证明:连接ON,OM,如图1,
∵N是
的中点,
∴NO⊥AB,
而OA=ON,
∴∠NAO=45°,
∴∠FAE=45°,
∵OM=OA,
∴∠AMO=45°,
∴△AOM为等腰直角三角形,
∴OA=
AM,
∵CD⊥AB,
∴△AEF为等腰直角三角形,
∴EF=AE,
∴EF+BE=AE+BE=AB,
而AB=2OA,
∴BE+EF=
AM;
(3)解:连接OC,BN,如图2,
∵EF=2CE=6,
∴CE=3,
在Rt△OCE中,OC=5,CE=3,
∴OE=
=4,
∴AE=OA+OE=9,
在Rt△AEF中,EF=6,AE=9,
∴AF=
=3
,
∵AB为⊙O的直径,
∴∠ANB=90°,
∵∠NAB=∠FAE,
∴Rt△ANB∽Rt△AEF,
∴
=
,即
=
,
∴AN=
.
 (1)证明:∵∠NAB=∠NGB,
(1)证明:∵∠NAB=∠NGB,而∠NGB=∠FAE,
∴∠NAB=∠FAE,
∴AB平分∠MAN;
(2)证明:连接ON,OM,如图1,
∵N是
 |
| AB |
∴NO⊥AB,
而OA=ON,
∴∠NAO=45°,
∴∠FAE=45°,
∵OM=OA,
∴∠AMO=45°,
∴△AOM为等腰直角三角形,
∴OA=
| ||
| 2 |

∵CD⊥AB,
∴△AEF为等腰直角三角形,
∴EF=AE,
∴EF+BE=AE+BE=AB,
而AB=2OA,
∴BE+EF=
| 2 |
(3)解:连接OC,BN,如图2,
∵EF=2CE=6,
∴CE=3,
在Rt△OCE中,OC=5,CE=3,
∴OE=
| 52-32 |
∴AE=OA+OE=9,
在Rt△AEF中,EF=6,AE=9,
∴AF=
| AE2+EF2 |
| 13 |
∵AB为⊙O的直径,
∴∠ANB=90°,
∵∠NAB=∠FAE,
∴Rt△ANB∽Rt△AEF,
∴
| AN |
| AE |
| AB |
| AF |
| AN |
| 9 |
| 10 | ||
3
|
∴AN=
30
| ||
| 13 |
点评:本题考查了圆的综合题:熟练掌握垂径定理及其推理、圆周角定理、圆内接四边形的性质和等腰直角三角形的判定与性质;会运用勾股定理和相似比进行几何计算.

练习册系列答案
相关题目
 某蓄水池的横断面示意图如图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )
某蓄水池的横断面示意图如图,分深水区和浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )



 如图,一张四边形纸片ABCD,AB∥CD,∠B=46°,把纸片一角沿折痕CN折叠,使BC与B′C′重合,过点C作CM⊥CN,试求∠BCM的度数.
如图,一张四边形纸片ABCD,AB∥CD,∠B=46°,把纸片一角沿折痕CN折叠,使BC与B′C′重合,过点C作CM⊥CN,试求∠BCM的度数. 如图,已知△ABC,AB=AC,∠BAC=90°,D为CB延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF.
如图,已知△ABC,AB=AC,∠BAC=90°,D为CB延长线上一点,连AD,以AD为边在△ABC的同侧作正方形ADEF. 如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF∥BC交AB于E、交AC于F.若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数.
如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF∥BC交AB于E、交AC于F.若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数.
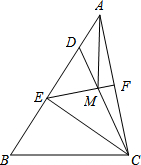 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.