题目内容
某电脑经销商计划购进一批电脑机箱和液晶显示器,已知购进电脑机箱10台和液晶显示器8台,共需要资金7000元;购进电脑机箱2台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商购进这两种商品50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)设每台电脑机箱、液晶显示器的进价各是x,y元,根据购进电脑机箱10台和液晶显示器8台,共需要资金7000元和电脑机箱2台和液晶显示器5台,共需要资金4120元,列出方程组,再进行求解即可;
(2)设该经销商购进电脑机箱m台,购进液晶显示器(50-m)台,根据购买这两种商品的资金不超过22240元和所获利润不少于4100元,列出不等式组,求出不等式组的解,即可得出答案.
(2)设该经销商购进电脑机箱m台,购进液晶显示器(50-m)台,根据购买这两种商品的资金不超过22240元和所获利润不少于4100元,列出不等式组,求出不等式组的解,即可得出答案.
解答:解:(1)设每台电脑机箱、液晶显示器的进价各是x,y元,
根据题意得:
,
解得:
.
答:每台电脑机箱、液晶显示器的进价各是60元,800元.
(2)设该经销商购进电脑机箱m台,购进液晶显示器(50-m)台,
根据题意得:
,
解得:24≤m≤26,
∵m要为整数,
∴m可以取24、25、26,
从而得出有三种进货方式:
①电脑箱:24台,液晶显示器:26台;
②电脑箱:25台,液晶显示器:25台;
③电脑箱:26台,液晶显示器:24台.
根据题意得:
|
解得:
|
答:每台电脑机箱、液晶显示器的进价各是60元,800元.
(2)设该经销商购进电脑机箱m台,购进液晶显示器(50-m)台,
根据题意得:
|
解得:24≤m≤26,
∵m要为整数,
∴m可以取24、25、26,
从而得出有三种进货方式:
①电脑箱:24台,液晶显示器:26台;
②电脑箱:25台,液晶显示器:25台;
③电脑箱:26台,液晶显示器:24台.
点评:此题考查了解二元一次方程组和一元一次不等式组,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系,列出方程组和不等式组.

练习册系列答案
相关题目
 如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF∥BC交AB于E、交AC于F.若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数.
如图,直线AB、CD交于点A,∠ABC的平分线BD与∠ACB的平分线交于点O,与AC交于点D;过点O作EF∥BC交AB于E、交AC于F.若∠BOC=125°,若∠ABC:∠ACB=3:2,求∠AEF和∠EFC的度数. 如图,在△ABC中,∠ABC=80°,∠ACB=50°.
如图,在△ABC中,∠ABC=80°,∠ACB=50°.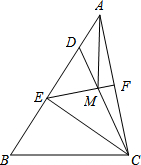 如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM.
如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M,连接AM. 如图,在△ABC中,AD是BC边上的高,BE平分∠BC交AD于点E,∠C=60°,∠BED=70°,求∠ABC和∠BAC的度数.
如图,在△ABC中,AD是BC边上的高,BE平分∠BC交AD于点E,∠C=60°,∠BED=70°,求∠ABC和∠BAC的度数. 如图是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
如图是某一蓄水池每小时的排水量V(m3/h)与排完水池中的水所用的时间t(h)之间的函数关系图象.
 如图,已知四边形ABCD是正方形,点E在DC上,将△ADE经顺时针旋转后与△ABF重合,再将△ABF向右平移后与△DCH重合.
如图,已知四边形ABCD是正方形,点E在DC上,将△ADE经顺时针旋转后与△ABF重合,再将△ABF向右平移后与△DCH重合. 如图,在直角梯形ABCD中,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为
如图,在直角梯形ABCD中,AB=BC=6,点E为BC边上一点,且∠EAD=45°,ED=5,则△ADE的面积为