题目内容
如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.
(1)当PQ∥AD时,求x的值;
(2)若线段PQ的垂直平分线与BC边相交于点M,设BM=y,求y关于x的函数关系式;
(3)若线段PQ的垂直平分线始终与BC边相交,求x的取值范围.

(1)当PQ∥AD时,求x的值;
(2)若线段PQ的垂直平分线与BC边相交于点M,设BM=y,求y关于x的函数关系式;
(3)若线段PQ的垂直平分线始终与BC边相交,求x的取值范围.

考点:矩形的性质,线段垂直平分线的性质,勾股定理
专题:动点型
分析:(1)根据矩形的性质可以求出AB=CD及AB∥CD,再有AD∥PQ可以得出四边形ADQP是平行四边形,由其性质就可以得出DQ=CQ,从而求出CQ的值而求出PA的值;
(2)根据中垂线的性质可以得出EP=EQ,由勾股定理就可以表示出EP2=PB2+BE2,EQ2=EC2+CQ2,由AP=x,BE=y,就可以表示出BP=8-x,EC=6-y,从而可以得出y与x之间的函数关系式;
(3)根据(2)可知y和x的函数关系式,因为线段PQ的垂直平分线始终与BC边相交,即0≤x≤6,由此可求出x的取值范围.
(2)根据中垂线的性质可以得出EP=EQ,由勾股定理就可以表示出EP2=PB2+BE2,EQ2=EC2+CQ2,由AP=x,BE=y,就可以表示出BP=8-x,EC=6-y,从而可以得出y与x之间的函数关系式;
(3)根据(2)可知y和x的函数关系式,因为线段PQ的垂直平分线始终与BC边相交,即0≤x≤6,由此可求出x的取值范围.
解答:解:(1)∵四边形ABCD是矩形,
∴AB∥CD,AB=CD=8.∠A=∠D=∠C=∠B=90°.
∵PQ∥AD,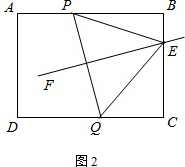
∴四边形ADQP是平行四边形,
∴AP=DQ.
∵AP=CQ,
∴DQ=CQ
∴DQ=
CD=4,
∴AP=4.
(2)如图2,∵EF是线段PQ的垂直平分线,
∴EP=EQ,
在Rt△BPE和Rt△ECQ中,由勾股定理,得
EP2=PB2+BE2,EQ2=EC2+CQ2,
∵AP=x,BE=y,
∴BP=8-x,EC=6-y.
∴(8-x)2+y2=(6-y)2+x2,
∴y=
;
(3)∵0≤y≤6,
∴0≤
≤6,
∴
≤x≤
.
∴AB∥CD,AB=CD=8.∠A=∠D=∠C=∠B=90°.
∵PQ∥AD,

∴四边形ADQP是平行四边形,
∴AP=DQ.
∵AP=CQ,
∴DQ=CQ
∴DQ=
| 1 |
| 2 |
∴AP=4.
(2)如图2,∵EF是线段PQ的垂直平分线,
∴EP=EQ,
在Rt△BPE和Rt△ECQ中,由勾股定理,得
EP2=PB2+BE2,EQ2=EC2+CQ2,
∵AP=x,BE=y,
∴BP=8-x,EC=6-y.
∴(8-x)2+y2=(6-y)2+x2,
∴y=
| 4x-7 |
| 3 |
(3)∵0≤y≤6,
∴0≤
| 4x-7 |
| 3 |
∴
| 7 |
| 4 |
| 25 |
| 4 |
点评:本题考查了矩形的性质的运用,平行四边形的性质的运用,中垂线的性质的运用,勾股定理的运用,题目的综合性较强,难度中等.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
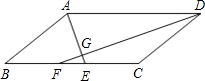 已知:如图,在?ABCD中,∠BAD,∠ADC的平分线AE、DF分别与线段BC相交于点E、F,AE与DF相交于点G.
已知:如图,在?ABCD中,∠BAD,∠ADC的平分线AE、DF分别与线段BC相交于点E、F,AE与DF相交于点G.
 如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
如图,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程: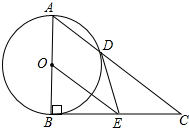 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.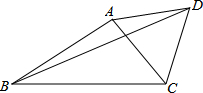 如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长.
如图,已知△ABC中,∠ABC=30°,AB=3,以AC为边向外作等边△ACD,BD=5.求BC长.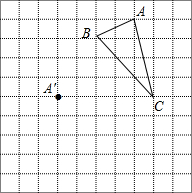 在正方形网格中,△ABC三个顶点的位置都在格点上如图所示,现将△ABC平移,使点A移动到点A′,点B′,点C′分别是B、C的对应点.
在正方形网格中,△ABC三个顶点的位置都在格点上如图所示,现将△ABC平移,使点A移动到点A′,点B′,点C′分别是B、C的对应点.