题目内容
(1)解方程:
=2+
;
(2)解不等式组
.并把解集在数轴上表示出来.
| 3x-5 |
| x-2 |
| x+1 |
| 2-x |
(2)解不等式组
|
考点:解一元一次不等式组,解分式方程,在数轴上表示不等式的解集
专题:
分析:(1)根据等式的性质先去掉分母,再去掉括号,然后移项、合并同类项,系数化1,再进行检验,即可得出答案;
(2)根据解不等式的步骤先分别求出每个不等式的解,再在数轴上表示出解集,即可得出答案.
(2)根据解不等式的步骤先分别求出每个不等式的解,再在数轴上表示出解集,即可得出答案.
解答:解:(1)
=2+
,
=2-
,
3x-5=2(x-2)-(x+1),
3x-5=2x-4-x-1,
2x=0,
x=0,
经检验x=0是方程的解,
则原方程的解是x=0;
(2)
,
由①得:x≤2,
由②得:x>1,
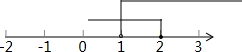
则原不等式组的解是:1<x≤2;
把不等式组的解集在数轴上表示为:
| 3x-5 |
| x-2 |
| x+1 |
| 2-x |
| 3x-5 |
| x-2 |
| x+1 |
| x-2 |
3x-5=2(x-2)-(x+1),
3x-5=2x-4-x-1,
2x=0,
x=0,
经检验x=0是方程的解,
则原方程的解是x=0;
(2)
|
由①得:x≤2,
由②得:x>1,
则原不等式组的解是:1<x≤2;
把不等式组的解集在数轴上表示为:

点评:此题考查了解分式方程和不等式组的解,掌握解分式方程的步骤和不等式组的解的步骤是本题的关键,注意分式方程要检验.

练习册系列答案
相关题目
下列运算中,正确的是( )
| A、x2+x2=x4 |
| B、x6÷x2=x3 |
| C、x2•x4=x6 |
| D、(3x2)2=6x4 |
 如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是
如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是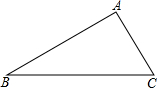 如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为
如图,在Rt△ABC中,∠A=90°,∠B=30°,BC=10,以A为圆心画圆,如果⊙A与直线BC相切,那么⊙A的半径长为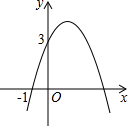 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
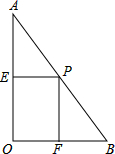 如图,在Rt△ABC中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一动点,PE⊥AO于点E,PF⊥BO于点F,设PE=x,矩形PFOE的面积为s.
如图,在Rt△ABC中,∠AOB=90°,且AO=8,BO=6,P是线段AB上一动点,PE⊥AO于点E,PF⊥BO于点F,设PE=x,矩形PFOE的面积为s.