题目内容
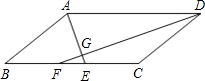 已知:如图,在?ABCD中,∠BAD,∠ADC的平分线AE、DF分别与线段BC相交于点E、F,AE与DF相交于点G.
已知:如图,在?ABCD中,∠BAD,∠ADC的平分线AE、DF分别与线段BC相交于点E、F,AE与DF相交于点G.(1)求证:AE⊥DF;
(2)若AD=10,AB=6,求EF的长.
考点:平行四边形的性质
专题:
分析:(1)根据平行四边形的性质和平行线的性质推出∠ADC+∠DAB=180°,根据角平分线得到∠ADF+∠DAE=
(∠ADC+∠DAB)=90°,即可求出结论;
(2)据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出FE的长.
| 1 |
| 2 |
(2)据平行四边形的性质和平行线的性质推出DC=FC,AB=EB,求出FE的长.
解答:(1)证明:在?ABCD中AB∥CD,
∴∠ADC+∠DAB=180°.
∵DF、AE分别是∠ADC、∠DAB的平分线,
∴∠ADF=∠CDF=
∠ADC,∠DAE=∠BAE=
∠DAB,
∴∠ADF+∠DAE=
(∠ADC+∠DAB)=90°,
∴∠AGD=90°,
∴AE⊥DF;
(2)?ABCD中AD∥BC,
∴∠ADF=∠CFD,∠DAE=∠BEA.
∴∠CDF=∠CFD,∠BAE=∠BEA.
∴DC=FC,AB=EB.
在?ABCD中,AD=BC=10,AB=DC=6,
∴CF=BE=6,BF=BC-CF=10-6=4.
∴FE=BE-BF=6-4=2,
∴∠ADC+∠DAB=180°.
∵DF、AE分别是∠ADC、∠DAB的平分线,
∴∠ADF=∠CDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ADF+∠DAE=
| 1 |
| 2 |
∴∠AGD=90°,
∴AE⊥DF;
(2)?ABCD中AD∥BC,
∴∠ADF=∠CFD,∠DAE=∠BEA.
∴∠CDF=∠CFD,∠BAE=∠BEA.
∴DC=FC,AB=EB.
在?ABCD中,AD=BC=10,AB=DC=6,
∴CF=BE=6,BF=BC-CF=10-6=4.
∴FE=BE-BF=6-4=2,
点评:本题主要考查对平行四边形的性质,三角形的内角和定理,平行线的性质,角平分线的定义,垂线的定义等知识点的理解和掌握,熟练地运用这些性质进行证明是解此题的关键,题型较好,综合性强.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
下列运算中,正确的是( )
| A、x2+x2=x4 |
| B、x6÷x2=x3 |
| C、x2•x4=x6 |
| D、(3x2)2=6x4 |
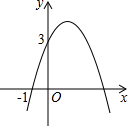 已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
已知二次函数y=-x2+bx+c的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).