题目内容
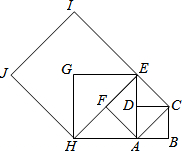 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….(1)记正方形ABCD的边长为a1=1,按上述方法所作的正方形的边长依次为a2,a3,a4,…,an,求出a4=
(2)根据以上规律写出第n个正方形的边长an的表达式
考点:正方形的性质
专题:规律型
分析:(1)根据正方形的性质得出∠B=90°,AB=BC=1,根据勾股定理求出即可;
(2)根据(1)中求出的结果得出规律,即可得出答案.
(2)根据(1)中求出的结果得出规律,即可得出答案.
解答:解:(1)∵四边形ABCD是正方形,
∴∠B=90°,AB=BC=1,
∴a1=1=(
)0,
由勾股定理得:a2=AC=
=
=(
)1,
同理由勾股定理得:a3=
=2=(
)2,
a4=
=2
,
故答案为:2
;
(2)∵a1=(
)0=1,a2=(
)1,a3=(
)2,a4=(
)3,…,
∴an=(
)n-1,
故答案为:an=(
)n-1.
∴∠B=90°,AB=BC=1,
∴a1=1=(
| 2 |
由勾股定理得:a2=AC=
| 12+12 |
| 2 |
| 2 |
同理由勾股定理得:a3=
(
|
| 2 |
a4=
| 22+22 |
| 2 |
故答案为:2
| 2 |
(2)∵a1=(
| 2 |
| 2 |
| 2 |
| 2 |
∴an=(
| 2 |
故答案为:an=(
| 2 |
点评:本题考查了正方形的性质,勾股定理的应用,解此题的关键是能根据求出的结果得出规律,题目比较好,难度适中.

练习册系列答案
相关题目
 如图,已知二次函数y=a(x-h)2+
如图,已知二次函数y=a(x-h)2+ 将一副三角板如图叠放,∠ABC=∠BCD=90°,∠A=45°,∠D=30°,若OB=2,则OD=
将一副三角板如图叠放,∠ABC=∠BCD=90°,∠A=45°,∠D=30°,若OB=2,则OD= 如图,有一直径是
如图,有一直径是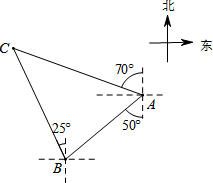 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= 学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下: