题目内容
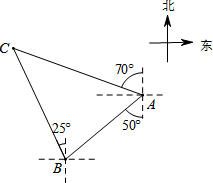 如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是
如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是| 2 |
| 3 |
| 6 |
考点:解直角三角形的应用-方向角问题
专题:几何图形问题
分析:作BD⊥AC于点D,在直角△ABD中,利用三角函数求得BD的长,然后在直角△BCD中,利用三角函数即可求得BC的长.
解答: 解:∠CBA=25°+50°=75°.
解:∠CBA=25°+50°=75°.
作BD⊥AC于点D.
则∠CAB=(90°-70°)+(90°-50°)=20°+40°=60°,
∠ABD=30°,
∴∠CBD=75°-30°=45°.
在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×
=10
.
在直角△BCD中,∠CBD=45°,
则BC=
BD=10
×
=10
≈10×2.4=24(海里).
故答案是:24.
 解:∠CBA=25°+50°=75°.
解:∠CBA=25°+50°=75°.作BD⊥AC于点D.
则∠CAB=(90°-70°)+(90°-50°)=20°+40°=60°,
∠ABD=30°,
∴∠CBD=75°-30°=45°.
在直角△ABD中,BD=AB•sin∠CAB=20×sin60°=20×
| ||
| 2 |
| 3 |
在直角△BCD中,∠CBD=45°,
则BC=
| 2 |
| 3 |
| 2 |
| 6 |
故答案是:24.
点评:本题主要考查了方向角含义,正确求得∠CBD以及∠CAB的度数是解决本题的关键.

练习册系列答案
相关题目
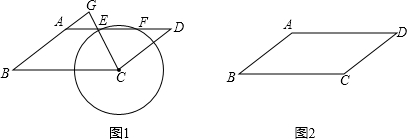
 如图,点D、E、F在△ABC三边上,EF、DG相交于点H,∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=50°,图中与△GFH相似的三角形的个数是
如图,点D、E、F在△ABC三边上,EF、DG相交于点H,∠ABC=∠EFC=70°,∠ACB=60°,∠DGB=50°,图中与△GFH相似的三角形的个数是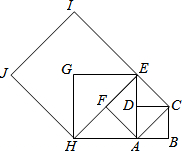 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去…. 如图,在平面直角坐标系xOy中,点A(
如图,在平面直角坐标系xOy中,点A(