题目内容
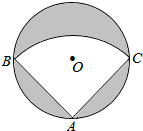 如图,有一直径是
如图,有一直径是| 2 |
(1)AB的长为
(2)用该扇形铁皮围成一个圆锥,所得圆锥的底面圆的半径为
考点:圆锥的计算,圆周角定理
专题:压轴题
分析:(1)根据圆周角定理由∠BAC=90°得BC为⊙O的直径,即BC=
,根据等腰直角三角形的性质得AB=1;
(2)由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,则2πr=
,然后解方程即可.
| 2 |
(2)由于圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,则2πr=
| 90•π•1 |
| 180 |
解答: 解:(1)∵∠BAC=90°,
解:(1)∵∠BAC=90°,
∴BC为⊙O的直径,即BC=
,
∴AB=
BC=1;
(2)设所得圆锥的底面圆的半径为r,
根据题意得2πr=
,
解得r=
.
故答案为:1,
.
 解:(1)∵∠BAC=90°,
解:(1)∵∠BAC=90°,∴BC为⊙O的直径,即BC=
| 2 |
∴AB=
| ||
| 2 |
(2)设所得圆锥的底面圆的半径为r,
根据题意得2πr=
| 90•π•1 |
| 180 |
解得r=
| 1 |
| 4 |
故答案为:1,
| 1 |
| 4 |
点评:本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了圆周角定理.

练习册系列答案
相关题目
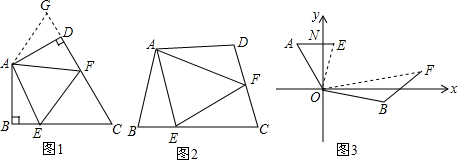
 如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去….
如图,设四边形ABCD是边长为1的正方形,以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以第二个正方形的对角线AE为边作第三个正方形AEGF,如此下去…. 如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则
如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则