题目内容
16.计算:(1)$\frac{12}{{m}^{2}-9}$+$\frac{2}{3-m}$;
(2)a+2-$\frac{4}{2-a}$;
(3)$\frac{2x-6}{x-2}$÷$\frac{x-3}{{x}^{2}-4x+4}$;
(4)$\frac{2x}{{x}^{2}-4}$-$\frac{1}{x-2}$.
分析 (1)利用平方差公式分解因式,再化为同分母求解即可,
(2)把分式化为同分母求解即可,
(3)先分解因式,再约分求解,
(4)利用平方差公式分解因式,再化为同分母求解即可.
解答 解:(1)$\frac{12}{{m}^{2}-9}$+$\frac{2}{3-m}$
=$\frac{12}{(m+3)(m-3)}$-$\frac{2(m+3)}{(m+3)(m-3)}$,
=$\frac{6-2m}{{m}^{2}-9}$;
(2)a+2-$\frac{4}{2-a}$
=$\frac{(a+2)(a-2)}{(a-2)}$+$\frac{4}{a-2}$,
=$\frac{{a}^{2}}{a-2}$;
(3)$\frac{2x-6}{x-2}$÷$\frac{x-3}{{x}^{2}-4x+4}$
=$\frac{2x-6}{x-2}$×$\frac{(x-2)^{2}}{x-3}$,
=2x-4;
(4)$\frac{2x}{{x}^{2}-4}$-$\frac{1}{x-2}$
=$\frac{2x}{(x+2)(x-2)}$-$\frac{x+2}{(x+2)(x-2)}$,
=$\frac{x-2}{(x+2)(x-2)}$,
=$\frac{1}{x+2}$.
点评 本题主要考查了分式的混合运算,解题的关键是正确的因式分解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
7.若二次函数y=x2-(2p+1)x-3p在-1≤x≤1的范围内至少有一个x的值使y≥0成立,则p的取值范围是( )
| A. | p>2 | B. | p>0 | C. | p≤2 | D. | 0<p≤2 |
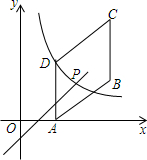 如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.
如图,四边形ABCD是平行四边形,点A(1,0),B(3,1),C(3,3),反比例函数y=$\frac{m}{x}$(x>0)的图象过点D,点P是一次函数y=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点.对于一次函数y=kx+3-3k(k≠0),当y随x的增大而增大时,则点P横坐标a的取值范围$\frac{2}{3}$<a<3.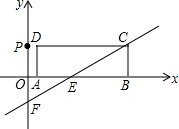 已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.
已知长方形ABCD的边长AB=9,AD=3,现将此长方形置于平面直角坐标系中,使AB在x轴的正半轴上,经过点C的直线y=$\frac{1}{2}$x-2与x轴交于点E,与y轴交于点F.