题目内容
15.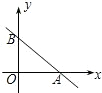 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.(1)求函数y=$-\frac{3}{4}$x+3的坐标三角形的三条边长;
(2)若函数y=$-\frac{3}{4}$x+b(b为常数)的坐标三角形周长为16,求函数关系式.
分析 (1)先求函数y=$-\frac{3}{4}$x+3与x、y轴的交点坐标,再求三角形的三边长;
(2)求得函数y=$-\frac{3}{4}$x+b与x、y轴的交点坐标,再求三角形的三边长,把三边的长加起来等于16,解方程求解即可求得b的值.
解答 解:(1)∵直线y=$-\frac{3}{4}$x+3与x轴的交点坐标为(4,0),与y轴交点坐标为(0,3),
∴函数y=$-\frac{3}{4}$x+3的坐标三角形的三条边长分别为3,4,5.
(2)直线y=$-\frac{3}{4}$x+b与x轴的交点坐标为($\frac{4}{3}$b,0),与y轴交点坐标为(0,b),
AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{b}^{2}+(\frac{4}{3}b)^{2}}$=$\frac{5}{3}$b,
当b>0时,b+$\frac{4}{3}$b+$\frac{5}{3}$b=16,得b=4;
当b<0时,-b-$\frac{4}{3}$b-$\frac{5}{3}$b=16,得b=-4,
所以函数关系式为y=$-\frac{3}{4}$x+4或y=$-\frac{3}{4}$x-4.
点评 本题考查了一次函数和几何问题的综合应用,本题中根据一次函数和坐标轴的交点坐标,求坐标三角形的三边长是解题的基础.

练习册系列答案
相关题目
 已知点E为菱形ABCD的边CD上任一点,AE、BC的延长线交于M,EF∥AD交DM于点F,说明:CE=EF.
已知点E为菱形ABCD的边CD上任一点,AE、BC的延长线交于M,EF∥AD交DM于点F,说明:CE=EF.