题目内容
8.若(b-2)2+$\sqrt{2a-b}$=0,则点M(a,b)关于y轴的对称点的坐标为(-1,2).分析 直接利用偶次方的性质以及二次根式的性质得出a,b的值,再利用关于y轴对称点的性质得出答案.
解答 解:∵(b-2)2+$\sqrt{2a-b}$=0,
∴$\left\{\begin{array}{l}{b-2=0}\\{2a-b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{a=1}\end{array}\right.$,
故点M(a,b)为(1,2),关于y轴的对称点的坐标为:(-1,2).
故答案为:(-1,2).
点评 此题主要考查了偶次方的性质以及二次根式的性质和关于y轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.

练习册系列答案
相关题目
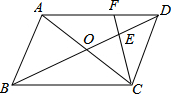 如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.
如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.