题目内容
10．在△ABC中，已知∠A+∠B=120°，∠B=$\frac{1}{2}$∠C，则∠C=60°，这个三角形是直角三角形．分析 先根据∠A+∠B=120°及三角形内角和定理求出∠C的度数，再由∠B=$\frac{1}{2}$∠C求出∠B的度数，进而得出∠A的度数，由此可得出结论．
解答 解：∵∠A+∠B=120°，∠A+∠B+∠C=180°，
∴∠C=180°-120°=60°．
∵∠B=$\frac{1}{2}$∠C，
∴∠B=$\frac{1}{2}$×60°=30°，
∴∠A=180°-∠B-∠C=180°-60°-30°=90°，
∴△ABC是直角三角形．
故答案为：60°，直角．
点评 本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
如图，点B、E、F、C在一条直线上，AB=DE=10，AC=DF，BE=CF=CE．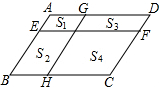
如图，EF和GH将?ABCD分成四个小平行四边形，设面积分别为S1=1，S2=3，S3=4，那么S4等于（ ）