题目内容
已知二次函数y=2x2-4mx+m2(m≠0).
(1)试说明这个二次函数的图象与x轴有两个交点;
(2)若这个二次函数的图象经过点(m+1,m),试确定该二次函数的表达式.
(1)试说明这个二次函数的图象与x轴有两个交点;
(2)若这个二次函数的图象经过点(m+1,m),试确定该二次函数的表达式.
考点:抛物线与x轴的交点
专题:
分析:(1)直接判断b2-4ac的符号,进而得出答案;
(2)将点(m+1,m),代入求出二次函数解析式即可.
(2)将点(m+1,m),代入求出二次函数解析式即可.
解答:解:(1)∵b2-4ac=16m2-4×2m2=8m2,m≠0,
∴b2-4ac=8m2>0,
∴这个二次函数的图象与x轴有两个交点;
(2)∵这个二次函数的图象经过点(m+1,m),
∴m=2(m+1)2-4m(m+1)+m2,
整理得:m2-m-2=0
(m-2)(m+1)=0
解得:m1=2,m2=-1,
故该二次函数的表达式为:y=2x2-8x+4或y=2x2+4x+1.
∴b2-4ac=8m2>0,
∴这个二次函数的图象与x轴有两个交点;
(2)∵这个二次函数的图象经过点(m+1,m),
∴m=2(m+1)2-4m(m+1)+m2,
整理得:m2-m-2=0
(m-2)(m+1)=0
解得:m1=2,m2=-1,
故该二次函数的表达式为:y=2x2-8x+4或y=2x2+4x+1.
点评:此题主要考查了抛物线与x轴交点问题,正确将已知点代入求出m的值是解题关键.

练习册系列答案
相关题目
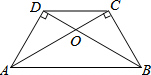 如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )| A、①②③④ | B、①②③ |
| C、①②④ | D、②③④ |
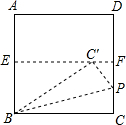 如图,先将正方形ABCD对折,折痕为EF,把这个正方形展开后,再将BC沿BP折叠,使点C落在EF上的点C′处,BP为折痕,则∠BPC的度数为( )
如图,先将正方形ABCD对折,折痕为EF,把这个正方形展开后,再将BC沿BP折叠,使点C落在EF上的点C′处,BP为折痕,则∠BPC的度数为( )| A、60° | B、67.5° |
| C、75° | D、80° |
 如图,在△ABC中点D是AC上一点,连接BD,点E是BD上一点,连接CE,求证:∠2+∠3=∠1-∠A.
如图,在△ABC中点D是AC上一点,连接BD,点E是BD上一点,连接CE,求证:∠2+∠3=∠1-∠A.