题目内容
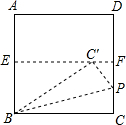 如图,先将正方形ABCD对折,折痕为EF,把这个正方形展开后,再将BC沿BP折叠,使点C落在EF上的点C′处,BP为折痕,则∠BPC的度数为( )
如图,先将正方形ABCD对折,折痕为EF,把这个正方形展开后,再将BC沿BP折叠,使点C落在EF上的点C′处,BP为折痕,则∠BPC的度数为( )| A、60° | B、67.5° |
| C、75° | D、80° |
考点:翻折变换(折叠问题)
专题:
分析:如图,首先求出∠BC′E=30°;证明∠CBC′=∠BC′E=30°;证明∠CBP=∠′BP=15°,问题即可解决.
解答: 解:如图,∵四边形ABCD为正方形,
解:如图,∵四边形ABCD为正方形,
∴BC=AB=λ;由题意得:
BE=
λ;BC′=BC=2λ,∠BEC′=90°;
∴BE=
BC′,∠BC′E=30°;
∵EF∥BC,
∴∠CBC′=∠BC′E=30°;
由题意得:∠CBP=∠′BP=15°,
∴∠BPC=90°-15°=75°,
故选C.
 解:如图,∵四边形ABCD为正方形,
解:如图,∵四边形ABCD为正方形,∴BC=AB=λ;由题意得:
BE=
| 1 |
| 2 |
∴BE=
| 1 |
| 2 |
∵EF∥BC,
∴∠CBC′=∠BC′E=30°;
由题意得:∠CBP=∠′BP=15°,
∴∠BPC=90°-15°=75°,
故选C.
点评:该题主要考查了翻折变换的性质及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答;对直觉判断能力提出了一定的要求.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
甲班有学生50人,乙班有学生45人,要使甲班人数是乙班人数的2倍,应从乙班调多少学生到甲班?设从乙班调出x人,则可列出的方程是( )
A、
| ||
| B、50-x=2(45+x) | ||
| C、50+2x=45 | ||
| D、50+x=2(45-x) |
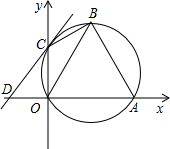 如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.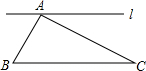 如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.
如图,已知∠A=90°,∠C=30°,AB=2,过点A的直线l与BC平行.若D是l上的一点,且BD=DC,求AD两点间的距离.