题目内容
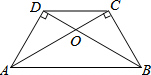 如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )
如图,∠ADB=∠ACB=90°,AC与BD交于点O,且AC=BD.有下列结论:①AD=BC;②∠DBC=∠CAD;③AO=BO;④AB∥CD.其中正确的是( )| A、①②③④ | B、①②③ |
| C、①②④ | D、②③④ |
考点:全等三角形的判定与性质
专题:
分析:由已知条件,得到三角形全等,得到结论,对每一个式子进行验证从而确定正确的式子.
解答:解:∵在Rt△ADB和Rt△BCA中
∴Rt△ADB≌Rt△BCA(HL)
∴AD=BC,∴①正确;
∠DAB=∠CBA,∠DBA=∠CAB
∴∠DBC=∠CAD,∴②正确;
在△AOD和△BOC中
∴△AOD≌△BOC(AAS)
∴AO=BO,∴③正确;
∵∠CDO+∠DCO+∠COD=180°,∠CDO=∠DCO,
∠OAB+∠OBA+∠AOB=180°,∠OAB=∠OBA
∠COD=∠AOB
∴∠DCO=∠OAB
∴AB∥CD,∴④正确;
所以以上结论都正确,
故选A.
|
∴Rt△ADB≌Rt△BCA(HL)
∴AD=BC,∴①正确;
∠DAB=∠CBA,∠DBA=∠CAB
∴∠DBC=∠CAD,∴②正确;
在△AOD和△BOC中
|
∴△AOD≌△BOC(AAS)
∴AO=BO,∴③正确;
∵∠CDO+∠DCO+∠COD=180°,∠CDO=∠DCO,
∠OAB+∠OBA+∠AOB=180°,∠OAB=∠OBA
∠COD=∠AOB
∴∠DCO=∠OAB
∴AB∥CD,∴④正确;
所以以上结论都正确,
故选A.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
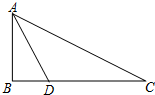 如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.
如图,△ABC中,∠B=90°,BC=8,BC上一点D,使BD:CD=3:5.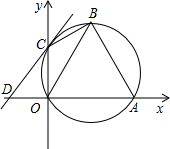 如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.
如图,直角坐标系中,已知两点O(0,0),A(2,0),点B在第一象限且△OAB为正三角形,△OAB的外接圆交y轴的正半轴于点C,过点C的圆的切线交x轴于点D.