题目内容
1. 如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.
如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.(1)求证:∠BAD=∠DAE;
(2)若AB=6,AD=5,求DF的长.
分析 (1)连接OD,由ED为⊙O的切线,根据切线的性质得到OD⊥ED,由AB为⊙O的直径,得到∠ACB=90°,根据平行线的判定和性质得到角之间的关系,又因为OA=OD,得到∠BAD=∠ADO,推出结论∠BAD=∠DAE;
(2)连接BD,得到∠ADB=90°,由勾股定理得到BD=$\sqrt{A{B^2}-A{D^2}}=\sqrt{11}$,根据三角函数的定义得到tan∠CBD=tan∠BAD=$\frac{{\sqrt{11}}}{5}$,由DF=BD•tan∠CBD=$\frac{11}{5}$.
解答 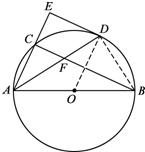 解:(1)连接OD,
解:(1)连接OD,
∵ED为⊙O的切线,
∴OD⊥ED,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC∥ED,
∴∠ACB=∠E=∠EDO,
∴AE∥OD,
∴∠DAE=∠ADO,
∵OA=OD,
∴∠BAD=∠ADO,
∴∠BAD=∠DAE;
(2)连接BD,
∴∠ADB=90°,
∵AB=6,AD=5,
∴BD=$\sqrt{A{B^2}-A{D^2}}=\sqrt{11}$,
∵∠BAD=∠DAE=∠CBD,
∴tan∠CBD=tan∠BAD=$\frac{{\sqrt{11}}}{5}$,
在Rt△BDF中,
∴DF=BD•tan∠CBD=$\frac{11}{5}$.
点评 本题考查了切线的性质,平行线的性质和判定,勾股定理,锐角三角函数,解题的关键是正确的作出辅助线.

练习册系列答案
相关题目
11.下列各式中,最简二次根式是( )
| A. | $\sqrt{\frac{1}{x-y}}$ | B. | $\frac{a}{b}$ | C. | $\sqrt{{x}^{2}+4}$ | D. | $\sqrt{5{a}^{2}b}$ |
12.已知点D与点A(-5,0),B(0,12),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )
| A. | 13 | B. | $\frac{13}{2}\sqrt{2}$ | C. | $\frac{17}{2}\sqrt{2}$ | D. | 12 |
10.已知0≤x≤$\frac{3}{2}$,则函数y=x2+x+1( )
| A. | 有最小值$\frac{3}{4}$,但无最大值 | B. | 有最小值$\frac{3}{4}$,有最大值1 | ||
| C. | 有最小值1,有最大值$\frac{19}{4}$ | D. | 无最小值,也无最大值 |
 如图,已知△ABC中BC=3cm,AC=4cm,AB=5cm,将△ABC绕AC旋转一周得到的几何体的侧面积为15π.
如图,已知△ABC中BC=3cm,AC=4cm,AB=5cm,将△ABC绕AC旋转一周得到的几何体的侧面积为15π.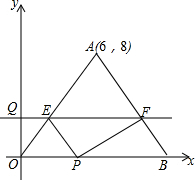 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).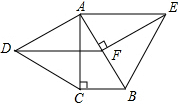 如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.
如图,分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE,已知∠BAC=30°,BC=1,EF⊥AB,垂足为F,连结DF.