题目内容
18.若直角三角形两直角边的比为3:4,斜边长为20,则此直角三角形的面积为96.分析 先根据比值设出直角三角形的两直角边,用勾股定理求出未知数x,即两条直角边,用面积公式计算即可.
解答 解:设直角三角形的两直角边分别为3x,4x(x>0),
根据勾股定理得,(3x)2+(4x)2=202,
∴x=4或x=-4(舍),
∴3x=12,4x=16
∴直角三角形的两直角边分别为12,16,
∴直角三角形的面积为$\frac{1}{2}$×12×16=96,
故答案为96.
点评 此题是勾股定理的应用,主要考查了勾股定理,三角形的面积计算方法,解本题的关键是用勾股定理求出直角边.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向,则∠ABC等于( )
如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向,则∠ABC等于( )
 如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向,则∠ABC等于( )
如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向,则∠ABC等于( )| A. | 40° | B. | 75° | C. | 35° | D. | 85° |
10. 如图,是对顶角量角器,则图中∠1等于( )
如图,是对顶角量角器,则图中∠1等于( )
 如图,是对顶角量角器,则图中∠1等于( )
如图,是对顶角量角器,则图中∠1等于( )| A. | 130° | B. | 140° | C. | 150° | D. | 160° |
7.在一次数学测试中,小明所在小组的8个同学的成绩(单位:分)分别是90,95,91,88,97,90,92,85,则这组数据的中位数是( )
| A. | 90 | B. | 90.5 | C. | 91 | D. | 92 |
8.下列说法正确的是( )
| A. | 4的平方根是2 | B. | $\root{3}{8}$是无理数 | ||
| C. | 无限小数都是无理数 | D. | 实数和数轴上的点一一对应 |
 如图,点G是矩形ABCD的边AD上一点,BG的垂直平分线EF经过点C.如果AG=1,AB=2,那么BC的长等于$\frac{5}{2}$.
如图,点G是矩形ABCD的边AD上一点,BG的垂直平分线EF经过点C.如果AG=1,AB=2,那么BC的长等于$\frac{5}{2}$.
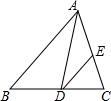 如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.
如图,已知AD是△ABC的角平分线,过点D作DE∥AB,交AC于点E,∠B=50°,∠ADE=30°,求∠C的度数.