题目内容
20. 如图所示,△ABC≌△ADE,点E、C、D恰好在同一直线上,若∠3=20°,试求∠2的度数.
如图所示,△ABC≌△ADE,点E、C、D恰好在同一直线上,若∠3=20°,试求∠2的度数.
分析 先由△ABC≌△ADE,根据全等三角形的对应角相等得出∠CAB=∠EAD,∠B=∠D,利用等式的性质得出∠CAB-∠CAD=∠EAD-∠CAD,即∠1=∠2.设AD与BC交于点O.根据三角形外角的性质得到∠BOD=∠1+∠B=∠3+∠D,而∠B=∠D,所以得出∠1=∠3,于是∠2=∠3=20°.
解答  解:∵△ABC≌△ADE,
解:∵△ABC≌△ADE,
∴∠CAB=∠EAD,∠B=∠D,
∴∠CAB-∠CAD=∠EAD-∠CAD,
∴∠1=∠2.
设AD与BC交于点O.
∵∠BOD=∠1+∠B=∠3+∠D,∠B=∠D,
∴∠1=∠3,
∴∠2=∠3=20°.
点评 本题考查了全等三角形对应角相等的性质,等式的性质,三角形外角的性质,难度适中.证明∠1=∠2,∠1=∠3是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,求证:CD=BC-AD.
如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,求证:CD=BC-AD.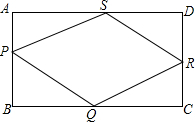 已知,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点在矩形边上.
已知,在矩形ABCD中,AB=4,BC=8,菱形PQRS的四个顶点在矩形边上. 已知:如图,在△ABC中,AD平分∠BAC,EF垂直平分AD.求证:∠B=∠CAF.
已知:如图,在△ABC中,AD平分∠BAC,EF垂直平分AD.求证:∠B=∠CAF.