题目内容
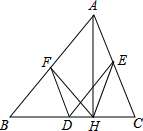 如图,在△ABC中,D,E,F分别为BC,AC,AB的中点.若AH⊥BC于点H,∠BAC=60°,则∠FDE=
如图,在△ABC中,D,E,F分别为BC,AC,AB的中点.若AH⊥BC于点H,∠BAC=60°,则∠FDE=考点:三角形中位线定理,直角三角形斜边上的中线
专题:
分析:根据三角形的中位线平行于第三边并且可得DF∥AC,DE∥AB,然后根据平行线的性质求出∠FDE=∠BAC;根据直角三角形斜边上的中线等于斜边的一半可得AF=FH,AE=EH,再根据等边对等角可得∠AHF=∠FAH,∠AHE=∠EAH,从而求出∠FHE=∠BAC.
解答:解:∵D,E,F分别为BC,AC,AB的中点,
∴DF∥AC,DE∥AB,
∴∠BFD=∠BAC,∠FDE=∠BFD,
∴∠FDE=∠BAC=60°,
∵AH⊥BC,E、F分别为AC、AB的中点,
∴AF=FH,AE=EH,
∴∠AHF=∠FAH,∠AHE=∠EAH,
∴∠AHF+∠AHE=∠FAH+∠EAH,
即∠FHE=∠BAC=60°.
故答案为:60°,60°.
∴DF∥AC,DE∥AB,
∴∠BFD=∠BAC,∠FDE=∠BFD,
∴∠FDE=∠BAC=60°,
∵AH⊥BC,E、F分别为AC、AB的中点,
∴AF=FH,AE=EH,
∴∠AHF=∠FAH,∠AHE=∠EAH,
∴∠AHF+∠AHE=∠FAH+∠EAH,
即∠FHE=∠BAC=60°.
故答案为:60°,60°.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
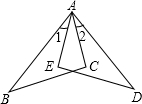 如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE. 如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE=
如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE= 如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是
如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是 如图,∠C=90°,若△ACD的周长为7cm,DE为AB边的垂直平分线,则AC+BC=
如图,∠C=90°,若△ACD的周长为7cm,DE为AB边的垂直平分线,则AC+BC=