题目内容
7.关于x的一元二次方程x2+2x+k+1=0的实数根是x1和x2(1)求k的取值范围;
(2)如果x1+x2-x1x2<-1,且k为整数,求k的值.
分析 (1)由方程有两个实数根,则其判别式大于或等于0可得到关于k的不等式,可求得k的取值范围;
(2)利用根与系数的关系表示出题目中的条件,结合(1)可求得k的取值范围,可求得k的值.
解答 解:(1)∵方程有两个实数根,
∴b2-4ac=22-4(k+1)≥0,
解得k≤0;
(2)由根与系数的关系可知:x1+x2=-2,x1x2=k+1,
∵x1+x2-x1x2<-1,
∴-2-(k+1)<-1,
∴k>-2,
由(1)知k≤0,
∴-2<k≤0,
∵k是整数,
∴k=-1或0.
点评 本题主要考查一元二次方程根的判别式及根与系数的关系,掌握一元二次方程有两个不相等的实数根?△>0、有两个相等的实数根?△=0和无实数根?△<0是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.$\sqrt{{a}^{2}}$等于( )
| A. | a | B. | -a | C. | ±a | D. | 以上都不对 |
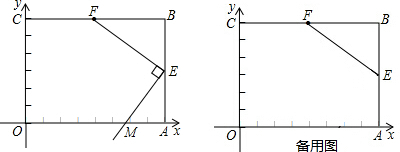
 如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.
如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.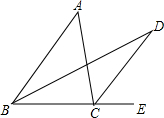 如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?
如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?