题目内容
18.如图,平面直角坐标系中,矩形OABC的顶点O在原点,点A在x轴的正半轴上,点C在y轴的正半轴上.已知E是AB的中点,F是BC的中点.(1)分别写出点E、点F的坐标;
(2)过点E作ME⊥EF交x轴于点M,求点M的坐标;
(3)在线段OC上是否存在点G,使得以点G、E、F为点的三角形是等腰三角形?若存在,求出点G的坐标;若不存在,请说明理由.
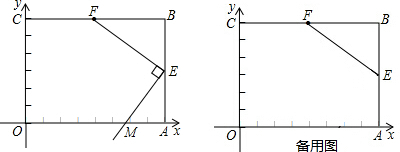
分析 (1)根据四边形OABC是矩形,OA=8,OC=6,E是AB的中点,F是BC的中点即可求出点E、点F的坐标;
(2)先利用相似三角形的性质求出△AEM∽△BFE,再由相似三角形的对应边成比例可求出AM的长,再根据OA=8即可求出OM的长,进而可求出M点的坐标;
(3)设G(0,n),过点P作GH⊥AB于点H,利用勾股定理可求出GF、GE、EF的长,再分GF=GE、GE=EF、GF=EF三种情况,列出方程求出n的值即可.
解答 解:(1)∵四边形OABC是矩形,OA=8,OC=6,E是AB的中点,F是BC的中点,
∴E(8,3),F(4,6);
(2)∵ME⊥EF,
∴∠BEF+∠AEM=90°,
∵∠BEF+∠BFE=90°,
∴∠AEM=∠BFE,
又∵∠EAM=∠B=90°,
∴△AEM∽△BFE,
∴$\frac{AM}{BE}$=$\frac{AE}{BF}$,
即$\frac{AM}{3}$=$\frac{3}{4}$,
∴AM=$\frac{9}{4}$,
∴OM=OA-AM=8-$\frac{9}{4}$=$\frac{23}{4}$,
∴M($\frac{23}{4}$,0);(9分)
(3)如图,
设G(0,n),
过点G作GH⊥AB于点H,
在Rt△CGF中,GF2=CF2+CG2=42+(6-n)2,
在Rt△EGH中,GE2=GH2+EH2=82+(3-n)2,
在Rt△BEF中,EF2=BE2+BF2=25,
①当GE=GF时GE2=GF2,
即82+(3-n)2=42+(6-n)2,
解得n=-$\frac{7}{2}$(不合题意,舍去);
②当GE=EF时GE2=EF2,
即82+(3-n)2=25,此方程无解;
③当GF=EF时GF2=EF2,
即42+(6-n)2=25,
解得n1=3,n2=9(不合题意,舍去),
综上,存在点G(0,3),此时△GEF是等腰三角形.
点评 此题考查四边形综合题,综合利用相似三角形的判定与性质、等腰三角形的性质、矩形的性质、勾股定理等知识解决问题.

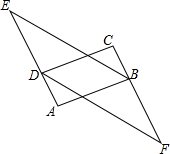 如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.
如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.