题目内容
 作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.(1)作出△A1B1C1和△A2B2C2;
(2)求出△A1B1C1旋转时扫过的面积.
考点:作图-旋转变换,扇形面积的计算
专题:作图题
分析:(1)根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可,再找出点A1、B1、C1绕点B1顺时针旋转90°后的对应点A2、B2、C2的位置,然后顺次连接即可;
(2)利用勾股定理列式求出A1B1,再根据△A1B1C1旋转扫过的面积=S扇形A1B1A2+S△A2B2C2列式计算即可得解.
(2)利用勾股定理列式求出A1B1,再根据△A1B1C1旋转扫过的面积=S扇形A1B1A2+S△A2B2C2列式计算即可得解.
解答: 解:(1)△A1B1C1和△A2B2C2如图所示;
解:(1)△A1B1C1和△A2B2C2如图所示;
(2)由勾股定理得,A1B1=
=5,
所以△A1B1C1旋转扫过的面积=S扇形A1B1A2+S△A2B2C2
=
+
×2×4
=
π+4.
 解:(1)△A1B1C1和△A2B2C2如图所示;
解:(1)△A1B1C1和△A2B2C2如图所示;(2)由勾股定理得,A1B1=
| 32+42 |
所以△A1B1C1旋转扫过的面积=S扇形A1B1A2+S△A2B2C2
=
| 90•π•52 |
| 360 |
| 1 |
| 2 |
=
| 25 |
| 4 |
点评:本题考查了利用旋转变换作图,利用平移变换作图,扇形的面积计算,熟练掌握网格结构准确找出对应点的位置是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,四边形OABC是正方形,点B的坐标是(6,6),D是边OA的中点,E是对角线OB上的一点,若AE+DE最小,则点E的坐标是( )
如图,四边形OABC是正方形,点B的坐标是(6,6),D是边OA的中点,E是对角线OB上的一点,若AE+DE最小,则点E的坐标是( )| A、(5,5) |
| B、(4,4) |
| C、(3,3) |
| D、(2,2) |
 如图,已知△ABC中,AB=AC=20cm,BC=16cm,点D为AB的中点.
如图,已知△ABC中,AB=AC=20cm,BC=16cm,点D为AB的中点. 如图,在?ABCD中,E,F为AC上两点,BE∥DF.求证:四边形BEDF为平行四边形.
如图,在?ABCD中,E,F为AC上两点,BE∥DF.求证:四边形BEDF为平行四边形.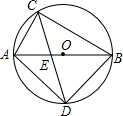 如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长.
如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长. 2014年3月8日马来西亚航班MH370失去联络,引起全世界的特别关注,来自各国搜救船队积极搜救,只为找到失联客机的相关线索.据报道3月22日在南印度洋某海域发现疑似飞机残骸,我国搜救队在接到信息后,立即制定相应搜救计划,并进行模拟,以提高搜救能力,如图是我国某搜救船队中甲、乙两组模拟海上搜救的示意图.已知甲在A点,乙在B点,其中点A位于点B南偏西75°处,AB=100海里,现在乙发现在它北偏西60°方向的点C处有疑似残骸,立即通知甲一起调查,并沿BC方向以12海里/小时前行,甲在接到通知后,调整位置,发现C在其北偏东45°方向,于是以20海里/小时的速度前往与乙汇合会合,请你计算,甲、乙能否同时到达C处?(参考数据:
2014年3月8日马来西亚航班MH370失去联络,引起全世界的特别关注,来自各国搜救船队积极搜救,只为找到失联客机的相关线索.据报道3月22日在南印度洋某海域发现疑似飞机残骸,我国搜救队在接到信息后,立即制定相应搜救计划,并进行模拟,以提高搜救能力,如图是我国某搜救船队中甲、乙两组模拟海上搜救的示意图.已知甲在A点,乙在B点,其中点A位于点B南偏西75°处,AB=100海里,现在乙发现在它北偏西60°方向的点C处有疑似残骸,立即通知甲一起调查,并沿BC方向以12海里/小时前行,甲在接到通知后,调整位置,发现C在其北偏东45°方向,于是以20海里/小时的速度前往与乙汇合会合,请你计算,甲、乙能否同时到达C处?(参考数据: