题目内容
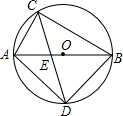 如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长.
如图,已知在⊙O中,直径AB为13cm,弦AC为5cm,∠ACB的平分线交⊙O于D,求BC,AD和BD的长.考点:圆周角定理,勾股定理
专题:
分析:根据题意可得出△ABC,△ABD是直角三角形,再根据勾股定理得出BC,根据等弧所对的圆周角相等可得出AD=BD,即可求出BD.
解答:解:∵⊙O直径AB为13cm,
∴∠ACB=∠ADB=90°,
∵弦AC为5cm,
∴BC=
=12cm,
∵∠ACB的平分线交⊙O于D,
∴
=
,
∴AD=BD,
∴在Rt△ADB中,AD2+BD2=AB2,
∵AB=13cm,
∴AD=BD=
cm.
∴∠ACB=∠ADB=90°,
∵弦AC为5cm,
∴BC=
| 132-52 |
∵∠ACB的平分线交⊙O于D,
∴
 |
| AD |
 |
| BD |
∴AD=BD,
∴在Rt△ADB中,AD2+BD2=AB2,
∵AB=13cm,
∴AD=BD=
13
| ||
| 2 |
点评:本题考查了圆周角定理,等腰直角三角形的性质及勾股定理,是基础知识比较简单.

练习册系列答案
相关题目
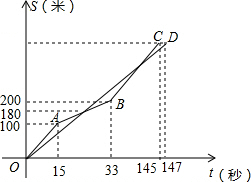 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
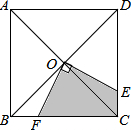 如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°.
如图,正方形ABCD的对角线AC、BD的交点为O,点E、F分别在CD、BC边上,且∠EOF=90°. 作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2. 如图,扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB的长为60cm,不贴纸部分AD的长是AB的
如图,扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB的长为60cm,不贴纸部分AD的长是AB的