题目内容
 如图,四边形OABC是正方形,点B的坐标是(6,6),D是边OA的中点,E是对角线OB上的一点,若AE+DE最小,则点E的坐标是( )
如图,四边形OABC是正方形,点B的坐标是(6,6),D是边OA的中点,E是对角线OB上的一点,若AE+DE最小,则点E的坐标是( )| A、(5,5) |
| B、(4,4) |
| C、(3,3) |
| D、(2,2) |
考点:轴对称-最短路线问题,坐标与图形性质,正方形的性质
专题:
分析:根据正方形的性质,点A、C关于OB对称,连接CD,根据轴对称确定最短路线问题,CD与OB的交点即为使AE+DE最小的点E,根据点B的坐标求出OB的长度,再根据△BCE和△ODE相似,利用相似三角形对应边成比例列式求出
=
=2,然后求出OE的长度,过点E作EF⊥OA于F,根据正方形的对角线平分一组对角可得∠AOB=45°,判断出△OEF是等腰直角三角形,然后根据等腰直角三角形的性质求出OF、EF,最后写出点E的坐标即可.
| BE |
| OE |
| BC |
| OD |
解答:解:∵四边形OABC是正方形,
∴点A、C关于OB对称,
连接CD,则CD与OB的交点即为使AE+DE最小的点E,
∵点B的坐标是(6,6),
∴OB=
=6
,
∵D是边OA的中点,
∴BC=OA=2OD,
∵BC∥OA,
∴△BCE∽△ODE,
∴
=
=2,
∴OE=6
×
=2
,
过点E作EF⊥OA于F,
∵∠AOB=45°,
∴△OEF是等腰直角三角形,
∴OF=EF=2
×
=2,
∴点E的坐标为(2,2).
故选D.
∴点A、C关于OB对称,
连接CD,则CD与OB的交点即为使AE+DE最小的点E,
∵点B的坐标是(6,6),
∴OB=
| 62+62 |
| 2 |
∵D是边OA的中点,
∴BC=OA=2OD,

∵BC∥OA,
∴△BCE∽△ODE,
∴
| BE |
| OE |
| BC |
| OD |
∴OE=6
| 2 |
| 1 |
| 1+2 |
| 2 |
过点E作EF⊥OA于F,
∵∠AOB=45°,
∴△OEF是等腰直角三角形,
∴OF=EF=2
| 2 |
| ||
| 2 |
∴点E的坐标为(2,2).
故选D.
点评:本题考查了轴对称确定最短路线问题,正方形的性质,相似三角形的判定与性质,等腰直角三角形的判定与性质,熟记各性质以及轴对称确定最短路线的方法确定出点E的位置并求出OE的长度是解题的关键.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )| A、4 | ||
B、
| ||
C、
| ||
D、
|
下列说法中,正确的是( )
A、若AC=
| ||
| B、若AC=BC,则C是AB的中点 | ||
| C、若C在线段AB上,且AC=BC,则C是AB的中点 | ||
D、若C在直线AB上,且AC=
|
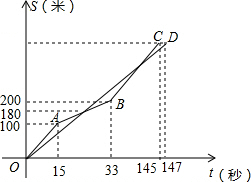 如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )
如图,在松雷中学学生跑步比赛中,甲、乙两学生跑步的路程s(米)与时间t(秒)之间的函数关系的图象分别为折线OABC和线段OD,下列说法正确的是( )| A、乙比甲先到终点 |
| B、比赛进行到29.4秒时,两人出发后第一次相遇 |
| C、乙测试的速度随时间增加而增大 |
| D、比赛全程甲的测试速度始终比乙的测试速度快 |
在平面直角坐标系中,点O是坐标原点,过点A(1,2)的直线y=kx+b与x轴交于点B,且S△AOB=4,则k的值是( )
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
 己知:如图,AD⊥BC,垂足为D,矩形EFGH的顶点都在△ABC的边上,且BC=36cm,AD=12cm,
己知:如图,AD⊥BC,垂足为D,矩形EFGH的顶点都在△ABC的边上,且BC=36cm,AD=12cm, 作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.