题目内容
7.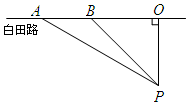 校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.(1)求A、B之间的路程;(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
(2)请判断此校车是否超过了白田路每小时60千米的限制速度?
分析 (1)分别在Rt△APO,Rt△BOP中,求得AO、BO的长,从而求得AB的长.已知时间则可以根据路程公式求得其速度.
(2)将限速与其速度进行比较,若大于限速则超速,否则没有超速.
解答 解:(1)在Rt△BOP中,∠BOP=90°,
∵∠BPO=45°,OP=100,
∴OB=OP=100.
在Rt△AOP中,∠AOP=90°,
∵∠APO=60°,
∴AO=OP•tan∠APO.
∴AO=100$\sqrt{3}$,
∴AB=100($\sqrt{3}$-1)(米);
(2)∵此车的速度=$\frac{100(\sqrt{3}-1)}{4}$=25($\sqrt{3}$-1)≈25×0.73=18.25米/秒,
60千米/小时=$\frac{60000}{3600}$≈16.67米/秒,
18.25米/秒>16,67米/秒,
∴此车超过了白田路每小时60千米的限制速度.
点评 本题考查了解直角三角形的应用,从复杂的实际问题中整理出直角三角形并求解是解决此类题目的关键.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
17.若分式$\frac{{\sqrt{2x-1}}}{x}$有意义,则x的取值范围是( )
| A. | x≥$\frac{1}{2}$ | B. | x≤$\frac{1}{2}$且x≠0 | C. | x≥$\frac{1}{2}$ | D. | x>$\frac{1}{2}$且x≠0 |
18.数据7,-7,0,6,-6,7的中位数和众数分别是( )
| A. | 6,-6 | B. | 3,7 | C. | 0,6 | D. | 0,7 |
12.经过点(2,-1)作一条直线和反比例函数y=$\frac{2}{x}$相交,当它们有且只有一个公共点时,这样的直线存在( )
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
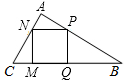 如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.
如图,已知△ABC中,∠BAC=90°,四边形PQMN是内接正方形.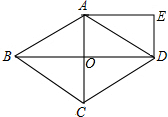 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长.