题目内容
13.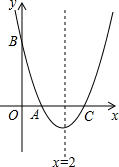 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)根据抛物线经过点A(1,0),对称轴是x=2列出方程组,解方程组求出b、c的值即可;
(2)因为点A与点C关于x=2对称,根据轴对称的性质,连接BC与x=2交于点P,则点P即为所求,求出直线BC与x=2的交点即可.
解答 解:(1)由题意得,$\left\{\begin{array}{l}{1-b+c=0}\\{\frac{b}{2}=2}\end{array}\right.$,
解得b=4,c=3,
∴抛物线的解析式为.y=x2-4x+3;
(2)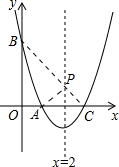 ∵点A与点C关于x=2对称,
∵点A与点C关于x=2对称,
∴连接BC与x=2交于点P,则点P即为所求,
根据抛物线的对称性可知,点C的坐标为(3,0),
y=x2-4x+3与y轴的交点为(0,3),
∴设直线BC的解析式为:y=kx+b,
$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得,k=-1,b=3,
∴直线BC的解析式为:y=-x+3,
则直线BC与x=2的交点坐标为:(2,1)
∴点P的坐标为:(2,1).
点评 本题考查的是待定系数法求二次函数的解析式和最短路径问题,掌握待定系数法求解析式的一般步骤和轴对称的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
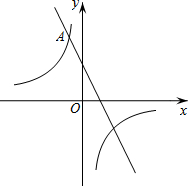 如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{m}{x}$与直线y=-2x+2交于点A(-1,a).
 如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).
如图,菱形ABCD中,对角线AC、BD相交于点O,不添加任何辅助线,请添加一个条件∠BAD=90°,使四边形ABCD是正方形(填一个即可).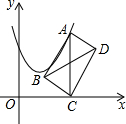 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.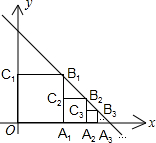 正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).
正方形OA1B1C1、A1A2B2C2、A2A3B3C3,按如图放置,其中点A1、A2、A3在x轴的正半轴上,点B1、B2、B3在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0).