题目内容
4.如图1是一把折叠椅子,图2是椅子完全打开支稳后的侧面示意图,其中AD和BC表示两根较粗的钢管,EG表示座板平面,EG和BC相交于点F,MN表示地面所在的直线,EG∥MN,EG距MN的高度为42cm,AB=43cm,CF=42cm,∠DBA=60°,∠DAB=80°.求两根较粗钢管AD和BC的长.(结果精确到0.1cm.参考数据:sin80°≈0.98,cos80°≈0.17,tan80°≈5.67,sin60°≈0.87,cos60°≈0.5,tan60°≈1.73)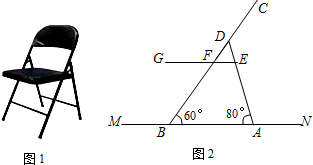
分析 作FH⊥AB于H,DQ⊥AB于Q,如图2,FH=42cm,先在Rt△BFH中,利用∠FBH的正弦计算出BF≈48.28,则BC=BF+CF=≈90.3(cm),再分别在Rt△BDQ和Rt△ADQ中,利用正切定义用DQ表示出BQ和AQ,得BQ=$\frac{DQ}{tan60°}$,AQ=$\frac{DQ}{tan80°}$,则利用BQ+AQ=AB=43得到$\frac{DQ}{tan60°}$+$\frac{DQ}{tan80°}$=43,解得DQ≈56.999,然后在Rt△ADQ中,利用sin∠DAQ的正弦可求出AD的长.
解答 解:作FH⊥AB于H,DQ⊥AB于Q,如图2,FH=42cm,
在Rt△BFH中,∵sin∠FBH=$\frac{FH}{BF}$,
∴BF=$\frac{42}{sin60°}$≈48.28,
∴BC=BF+CF=48.28+42≈90.3(cm); 在Rt△BDQ中,∵tan∠DBQ=$\frac{DQ}{BQ}$,
在Rt△BDQ中,∵tan∠DBQ=$\frac{DQ}{BQ}$,
∴BQ=$\frac{DQ}{tan60°}$,
在Rt△ADQ中,∵tan∠DAQ=$\frac{DQ}{AQ}$,
∴AQ=$\frac{DQ}{tan80°}$,
∵BQ+AQ=AB=43,
∴$\frac{DQ}{tan60°}$+$\frac{DQ}{tan80°}$=43,解得DQ≈56.999,
在Rt△ADQ中,∵sin∠DAQ=$\frac{DQ}{AD}$,
∴AD=$\frac{56.999}{sin80°}$≈58.2(cm).
答:两根较粗钢管AD和BC的长分别为58.2cm、90.3cm.
点评 本题考查了解直角三角形的应用:将实际问题抽象为数学问题(画出平面图形,构造出直角三角形转化为解直角三角形问题).根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | y=$\frac{1}{2}$x+1 | B. | y=$\frac{1}{2}$x-1 | C. | y=-$\frac{1}{2}$x-1 | D. | y=-$\frac{1}{2}$x+1 |
| A. | -6a6b3 | B. | -8a6b3 | C. | 8a6b3 | D. | -8a5b3 |
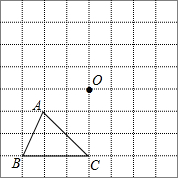 如图,在方格网中已知格点△ABC和点O.
如图,在方格网中已知格点△ABC和点O.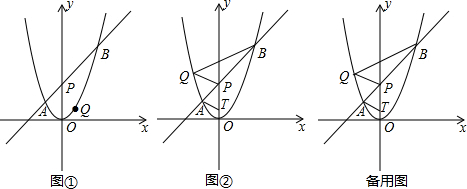
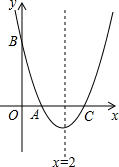 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.