题目内容
2.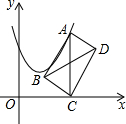 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为1.
分析 先利用配方法得到抛物线的顶点坐标为(1,1),再根据矩形的性质得BD=AC,由于AC的长等于点A的纵坐标,所以当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,从而得到BD的最小值.
解答 解:∵y=x2-2x+2=(x-1)2+1,
∴抛物线的顶点坐标为(1,1),
∵四边形ABCD为矩形,
∴BD=AC,
而AC⊥x轴,
∴AC的长等于点A的纵坐标,
当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,
∴对角线BD的最小值为1.
故答案为1.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了矩形的性质.

练习册系列答案
相关题目
14.计算(-2a2b)3的结果是( )
| A. | -6a6b3 | B. | -8a6b3 | C. | 8a6b3 | D. | -8a5b3 |
11.若a与1互为相反数,则|a+1|等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
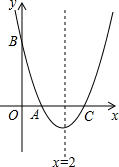 如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
如图,抛物线y=x2-bx+c交x轴于点A(1,0),交y轴于点B,对称轴是x=2.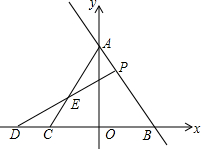 如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E
如图,在平面直角坐标系中,直线l:y=-$\frac{4}{3}$x+4与y轴、x轴分别交于点A、B,若点C是x轴负半轴上一点,当AB=BC时,点P在线段AB上,点Q是x轴负半轴上一点(在点C的左侧),且AP=CQ,PQ与线段AC交于点E