题目内容
 如图,在?ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
如图,在?ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB=
| 3 |
| 2 |
考点:平行四边形的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:几何综合题
分析:(1)根据平行四边形的性质可得AB∥CN,由此可知∠B=∠ECN,再根据全等三角形的判定方法ASA即可证明△ABE≌△NCE;
(2)因为AB∥CN,所以△AFG∽△CNG,利用相似三角形的性质和已知条件即可得到含n的式子表示线段AN的长.
(2)因为AB∥CN,所以△AFG∽△CNG,利用相似三角形的性质和已知条件即可得到含n的式子表示线段AN的长.
解答:(1)证明:
∵四边形ABCD是平行四边形,
∴AB∥CN,
∴∠B=∠ECN,
∵E是BC中点,
∴BE=CE,
在△ABE和△NCE中,
,
∴△ABE≌△NCE(ASA).
(2)∵AB∥CN,
∴△AFG∽△CNG,
∴AF:CN=AG:GN,
∵AB=CN,
∴AF:AB=AG:GN,
∵AB=3n,F为AB中点
∴FB=
GE,
∴GE=n,
∴
=
,解得AE=3n,
∴AG=2n,GE=n,EN=3n,
∴AN=AG+GE+EN=2n+n+3n=6n.
∵四边形ABCD是平行四边形,
∴AB∥CN,
∴∠B=∠ECN,
∵E是BC中点,
∴BE=CE,
在△ABE和△NCE中,
|
∴△ABE≌△NCE(ASA).
(2)∵AB∥CN,

∴△AFG∽△CNG,
∴AF:CN=AG:GN,
∵AB=CN,
∴AF:AB=AG:GN,
∵AB=3n,F为AB中点
∴FB=
| 3 |
| 2 |
∴GE=n,
∴
| ||
| 3n |
| AE-n |
| AE+n |
∴AG=2n,GE=n,EN=3n,
∴AN=AG+GE+EN=2n+n+3n=6n.
点评:本题考查了平行四边形的性质、全等三角形的判定和性质以及相似三角形的平和性质,题目的综合性较强,难度中等.

练习册系列答案
相关题目
下列各组运算中,结果为负数的是( )
| A、-|-2| |
| B、(-3)×(-4) |
| C、-(-2) |
| D、(-1)2 |
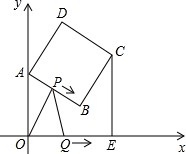 如图,在正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限,动点P在正方形ABCD的边上从点A出发沿A→B→C以每秒一个单位长度匀速运动,同时动点Q以每秒
如图,在正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限,动点P在正方形ABCD的边上从点A出发沿A→B→C以每秒一个单位长度匀速运动,同时动点Q以每秒
