题目内容
某旅游景点的门票价格是20元/人,日接待游客500人,进入旅游旺季时,景点想提高门票价格增加盈利.经过市场调查发现,门票价格每提高5元,日接待游客人数就会减少50人.设提价后的门票价格为x(元/人)(x>20),日接待游客的人数为y(人).
(1)求y与x(x>20)的函数关系式;
(2)已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;
(3)在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入-接待成本)
(1)求y与x(x>20)的函数关系式;
(2)已知景点每日的接待成本为z(元),z与y满足函数关系式:z=100+10y.求z与x的函数关系式;
(3)在(2)的条件下,当门票价格为多少时,景点每日获取的利润最大?最大利润是多少?(利润=门票收入-接待成本)
考点:二次函数的应用
专题:应用题
分析:(1)根据门票价格每提高5元,日接待游客人数就会减少50人,可得价格与人数的关系;
(2)根据成本与人数的关系式,可得函数解析式;
(3)根据二次函数的性质,a<0,当自变量取-
时,函数取最大值,可得答案.
(2)根据成本与人数的关系式,可得函数解析式;
(3)根据二次函数的性质,a<0,当自变量取-
| b |
| 2a |
解答:解:(1)由题意得y=500-50×
,
即y=-10x+700;
(2)由z=100+10y,y=-10x+700,得
z=-100x+7100;
(3)w=x(-10x+700)-(-100x+7100)
即w=-10x2+800x-7100,
当x=-
=-
=40时,景点每日获取的利润最大,
w最大=
=
=8900(元),
答:当门票价格为40元时,景点每日获取的利润最大,最大利润是8900元.
| x-20 |
| 5 |
即y=-10x+700;
(2)由z=100+10y,y=-10x+700,得
z=-100x+7100;
(3)w=x(-10x+700)-(-100x+7100)
即w=-10x2+800x-7100,
当x=-
| b |
| 2a |
| 800 |
| 2×(-10) |
w最大=
| 4ac-b2 |
| 4a |
| 4×(-10)×(-7100)-8002 |
| 4×(-10) |
答:当门票价格为40元时,景点每日获取的利润最大,最大利润是8900元.
点评:本题考查了二次函数的应用,列函数解析式是解题关键,利用了二次函数的性质.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
若三角形的边长为3、4、5,那么连结各边中点所成的三角形的周长为( )
| A、6 | B、6.5 | C、7 | D、8 |
下列说法中,不正确的个数是( )
①如果两个角相等,那么这两个角是对顶角;
②在同一平面内,不相交的两条线段叫平行线;
③经过一点有且只有一条直线平行于已知直线;
④两条直线被第三条直线所截,同位角相等.
①如果两个角相等,那么这两个角是对顶角;
②在同一平面内,不相交的两条线段叫平行线;
③经过一点有且只有一条直线平行于已知直线;
④两条直线被第三条直线所截,同位角相等.
| A、1个 | B、2个 | C、3个 | D、4个 |
如果a+b+c=0,且|a|>|b|>|c|,则下列说法中可能成立的是( )
| A、a、b为正数,c为负数 |
| B、a、c为正数,b为负数 |
| C、b、c为正数,a为负数 |
| D、a、c为负数,b为正数 |
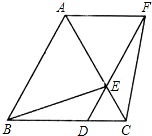 如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,连接AF.
如图,已知△ABC是等边三角形,E为AC上一点,连接BE.将△BEC旋转,使点C落在BC上的点D处,点B落在BC上方的点F处,连接AF.
 如图,在?ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
如图,在?ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N. 如图,点E是正方形内一点,△EDC是等边三角形
如图,点E是正方形内一点,△EDC是等边三角形