题目内容
12．因式分解：x2+2xy+y2-z2=（x+y+z）（x+y-z）．分析 前3项分成一组利用完全平方公式分解，然后再与第四项利用平方差公式分解因式．
解答 解：原式=（x2+2xy+y2）-z2
=（x+y）2-z2
=（x+y+z）（x+y-z）．
故答案是：（x+y+z）（x+y-z）．
点评 本题考查了分组分解法分解因式，难点是采用两两分组还是三一分组．比如本题有a的二次项，a的一次项，有常数项，所以首要考虑的就是三一分组．
练习册系列答案
相关题目
2．已知关于x的一元二次方程x2-2（m+1）x+m2-3=0．
（1）求使方程有两实数根的实数m的取值范围．
（2）若方程的两实数根为x1、x2，且（x1+x2）2-（x1+x2）-12=0，求m的值．
（1）求使方程有两实数根的实数m的取值范围．
（2）若方程的两实数根为x1、x2，且（x1+x2）2-（x1+x2）-12=0，求m的值．
3．计算：c-[d-2c-（c-d）]等于（ ）
| A． | -2d | B． | 2c | C． | 2d-2c | D． | 4c-2d |
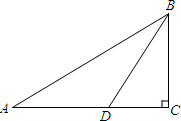如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，tan A=$\frac{\sqrt{3}}{3}$，AD=20．求BC的长．