题目内容
16.如图1,在以O为原点的平面直角坐标系中,点A的坐标为(0,2),点P(s,t)在抛物线y=$\frac{1}{4}$x2+1上,点P到x轴的距离记为m,PA=n.(1)若s=4,分别求出m、n的值,并比较m与n的大小关系;
(2)若点P是该抛物线上的一个动点,则(1)中m与n的大小关系是否仍成立?请说明理由;
(3)如图2,过点P的直线y=kx(k≠0)与抛物线交于另一点Q连接PA、QA,是否存在k使得PA=2QA?若存在,请求出k的值;若不存在,请举例说明.
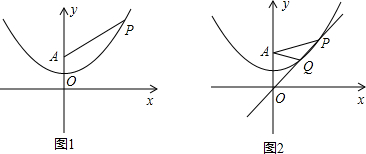
分析 (1)根据抛物线上点的横坐标代入抛物线解析式中,求出t=5,再用两点间的距离公式求出PA,即可;
(2)设出点P(S,$\frac{1}{4}$S2+1),求出m,n即可;
(3)分别过P、Q作PN⊥x轴,QM⊥x轴,由△QOM∽△PON得到ON=2OM,由PN=2QM建立方程,$\frac{1}{4}$(2a)2+1=2($\frac{1}{4}$a2+1),求出a=$±\sqrt{2}$,再分两种情况计算即可.
解答 解:(1)∵当s=4时,点P(s,t)在抛物线y=$\frac{1}{4}$x2+1上,
∴t=5,
∵点P到x轴的距离记为m,
∴m=5,
∴P(4,5)
∵A(0,2),
∴PA=$\sqrt{(4-0)^{2}+(5-2)^{2}}$=5,
∴m=n,
∴m=5,n=5,m=n,
(2)m=n 仍然成立.
设P(s,$\frac{1}{4}$s2+1),
∴m=$\frac{1}{4}$s2+1,
∴n=$\sqrt{{s}^{2}+(\frac{1}{4}{{s}^{2}+1-2)}^{2}}$=$\frac{1}{4}$s2+1,
∴m=n 仍然成立;
(3)如图,
分别过P、Q作PN⊥x轴,QM⊥x轴,
∵PA=2QA,
由(2)知,PN=2QM,
∵△QOM∽△PON,
∴ON=2OM,
设Q(a,$\frac{1}{4}$a2+1),
∴P[2a,$\frac{1}{4}$(2a)2+1],
由PN=2QM得,$\frac{1}{4}$(2a)2+1=2($\frac{1}{4}$a2+1),
∴a=$±\sqrt{2}$,
当a=$\sqrt{2}$时,
∴P(2$\sqrt{2}$,3),
∴k=$\frac{3\sqrt{2}}{4}$;
当a=-$\sqrt{2}$时,
∴∴P(-2$\sqrt{2}$,3),
∴k=-$\frac{3\sqrt{2}}{4}$;
∴k=±$\frac{3\sqrt{2}}{4}$.
点评 此题是二次函数综合题,主要考查了确定抛物线上点的坐标,相似三角形的性质和判定,解本题的关键是找相等关系建立方程.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | -4 | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | 4 |
| 甲方案 | 乙方案 | |
| 门号的月租费(元) | 400 | 600 |
| MAT手机价格(元) | 15000 | 13000 |
| 注意事项:以上方案两年内不可变更月租费 | ||
| A. | 500 | B. | 516 | C. | 517 | D. | 600 |
 如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.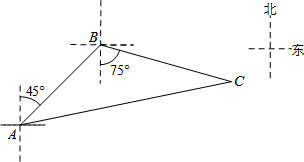 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.