题目内容
7. 如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
如图,在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF⊥AC分别交AD、AB于点E、F,将△AEF沿EF折叠,点A落在点A′处,当△A′BC是等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
分析 首先证明四边形AEA′F是菱形,分两种情形:①CA′=CB,②A′C=A′B分别计算即可.
解答 解:∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,∠DAC=∠BAC,
∵EF⊥AA′,
∴∠EPA=∠FPA=90°,
∴∠EAP+∠AEP=90°,∠FAP+∠AFP=90°,
∴∠AEP=∠AFP,
∴AE=AF,
∵△A′EF是由△AEF翻折,
∴AE=EA′,AF=FA′,
∴AE=EA′=A′F=FA,
∴四边形AEA′F是菱形,
∴AP=PA′
①当CB=CA′时,∵AA′=AC-CA′=3,∴AP=$\frac{1}{2}$AA′=$\frac{3}{2}$.
②当A′C=A′B时,∵∠A′CB=∠A′BC=∠BAC,
∴△A′CB∽△BAC,
∴$\frac{A′C}{AB}$=$\frac{BC}{AC}$,
∴A′C=$\frac{25}{8}$,
∴AA=8-$\frac{25}{8}$=$\frac{39}{8}$,
∴AP=$\frac{1}{2}$AA′=$\frac{39}{16}$.
故答案为$\frac{3}{2}$或$\frac{39}{16}$.
点评 本题考查菱形的性质、翻折变换、等腰三角形的判定和性质等知识,解题的关键是学会分类讨论,不能漏解,属于中考常考题型.

练习册系列答案
相关题目
3.下列长度的三条线段能组成钝角三角形的是( )
| A. | 3,4,4 | B. | 3,4,5 | C. | 3,4,6 | D. | 3,4,7 |
15.用科学记数法表示的数6.18×10-3,其原数为( )
| A. | 0.618 | B. | 0..618 | C. | 0.00618 | D. | 0.000618 |
 如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.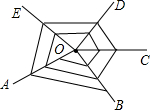 如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.
如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.