题目内容
 将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=
将矩形纸片ABCD如图那样折叠,使顶点B与顶点D重合,折痕为EF.若∠DFC=70°,则∠DEF=考点:翻折变换(折叠问题)
专题:计算题
分析:根据折叠的性质可知Rt△A′DE≌Rt△CDF,故有DE=DF,∠DEF=∠DFE;∠DFC=70°,∠DFE=∠BFE=55°,继而即可得出答案.
解答:解:根据折叠的性质可知:四边形ABFE和四边形A′DFE全等,
∴∠A′=∠A=90°,∠DFE=∠BFE,A′D=AB=CD,
在Rt△A′DE和Rt△CDF中,
,
∴Rt△A′DE≌Rt△CDF,
∴DE=DF,
∴∠DEF=∠DFE,
∵∠DFC=70°,
∴∠DFE=∠BFE=55°,
∴∠DEF=55°.
故答案为:55.
∴∠A′=∠A=90°,∠DFE=∠BFE,A′D=AB=CD,
在Rt△A′DE和Rt△CDF中,
|
∴Rt△A′DE≌Rt△CDF,
∴DE=DF,
∴∠DEF=∠DFE,
∵∠DFC=70°,
∴∠DFE=∠BFE=55°,
∴∠DEF=55°.
故答案为:55.
点评:本题考查翻折变换的知识,解题关键是证得DE=DF,注意掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等,难度一般.

练习册系列答案
相关题目
当2x-3>0时,|x-1|+
=( )
| 9-12x+4x2 |
| A、x-2 | B、3x-4 |
| C、2-x | D、4-3x |
 如图,正比例函数
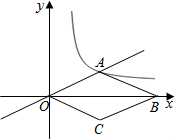
如图,正比例函数 在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.
在△ABC中,已知,DE∥BC,则S△ADE:S梯形BCED=1:8.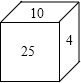 如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?
如图,有一个正方体木块,每个面上写了一个自然数,并且相对的两个面上的数字之和都相等.现在只能看到三个面上写的数字,如果看不见的三个面上写的都是质数,那么这三个质数是?