题目内容
5.已知实数x、y满足方程x2-3xy+3y2+4x-18y+52=0,则yx的个位数字是4.分析 首先把原方程看作关于x的方程,进一步利用根的判别式求得y的取值范围,进一步求得y的数值,再求得x的数值,进一步利用位数特征求得答案即可.
解答 解:∵数x、y满足方程x2-3xy+3y2+4x-18y+52=0,
∴x2+(4-3y)x+3y2-18y+52=0,
∴△=(4-3y)2-4(+3y2-18y+52)=16-24y+9y2-12y2+72y-208=-3(y-8)2≥0,
∴(y-8)2≤0,
∴y=8,
把y=8代入原方程求得x=10,
∴yx=810
81个位数字是8,
82个位数字是4,
83个位数字是2.
84个位数字是6,
85个位数字是8,
…
810个位数字是4.
故答案为:4.
点评 此题考查配方法的运用,非负数的性质,根的判别式以及乘方的尾数特征,根据题目特点,灵活转化问题的思路与方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16. 如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
 如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )
如图,在平行四边形纸片ABCD中,BC=4$\sqrt{3}$,将纸片沿对角线AC对折,BC边与AD边交于点E,此时,△CDE恰为等边三角形,则重叠面积为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图所示,在一次敌我双方交战中,我军先头部队在距敌方据点A处200米的B处遇到敌方火力阻击,为了尽快扫除障碍,使我军在C处的后续大部队顺利前进,先头部队请求大部队炮火支援,如果你就在先头部队中,你能表述出敌方据点的准确位置吗?
如图所示,在一次敌我双方交战中,我军先头部队在距敌方据点A处200米的B处遇到敌方火力阻击,为了尽快扫除障碍,使我军在C处的后续大部队顺利前进,先头部队请求大部队炮火支援,如果你就在先头部队中,你能表述出敌方据点的准确位置吗?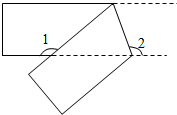 将一个宽度相等的纸条按如图所示方式折叠,如果∠1=138°,那么∠2=111°.
将一个宽度相等的纸条按如图所示方式折叠,如果∠1=138°,那么∠2=111°. 已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?
已知,在四边形ABCD中,点E为AB上的任一点,过E作EF∥AD交BD于点F,过F作FG∥CD交BC于点G,EG与AC平行吗,为什么?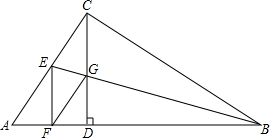 如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB.
如图,已知在Rt△ABC中,CD是斜边AB上的高,∠ABC的平分线BE交CD于点G,交AC于点E,GF∥AC交AB于点F.求证:EF⊥AB. 如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.
如图,点A、C、B、D在同一条直线上,AC=BD,AM∥CN,BM∥DN,那么AM与CN相等吗?请你说明理由.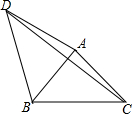 已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则四边形ACBD的面积为22.
已知:如图,等腰直角△ABC,∠BAC=90°,AB=AC,点D为△ABC外一点,∠ADB=45°,连接CD,AD=4$\sqrt{2}$,CD=10,则四边形ACBD的面积为22.