题目内容
15.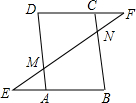 如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.
如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.
分析 观察图形,可猜测全等的三角形应该是△EBN≌△FDM和△△EAM≌△FCN,然后着手证明即可.
解答 解:可猜测全等的三角形应该是△EBN≌△FDM和△△EAM≌△FCN,
理由如下:
①∵?ABCD中,AB∥CD,∠B=∠D,AB=CD,
∴∠E=∠F,
又∵AE=CF,
∴BE=DF,
在△EBN和△FDM中,
$\left\{\begin{array}{l}{∠E=∠F}\\{BE=DF}\\{∠B=∠D}\end{array}\right.$,
∴△EBN≌△FDM;
②∵?ABCD中,AB∥CD,∠DAB=∠BCD,
∴∠E=∠F,∠EAM=∠FCN,
又∵AE=CF,
在△EAM和△FCN中,
$\left\{\begin{array}{l}{∠E=∠F}\\{AE=CF}\\{∠EAM=∠FCN}\end{array}\right.$,
∴△EAM≌△FCN.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定,属于基础题,难度不大.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
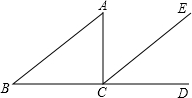 如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°.如果∠B=36°,求∠ACE的度数.
如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°.如果∠B=36°,求∠ACE的度数.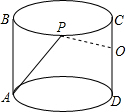 如图所示,已知一个圆柱体杯子高为6,直径为$\frac{18}{π}$,点O是CD的中点,一只蚂蚁在A处(杯子外面),想吃到杯子内部点O处的糖,当P在何处即PC=3时,蚂蚁爬行的路程最短.
如图所示,已知一个圆柱体杯子高为6,直径为$\frac{18}{π}$,点O是CD的中点,一只蚂蚁在A处(杯子外面),想吃到杯子内部点O处的糖,当P在何处即PC=3时,蚂蚁爬行的路程最短.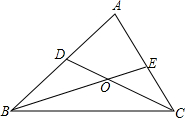 如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O.
如图所示,在△ABC中,∠ABC和∠ACB的平分线BE和CD相交于点O. 若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求:
若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求: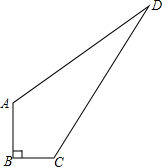 如图,∠B=90°,AB=3,BC=4,AD=12,BD=13,求四边形ABCD的面积.
如图,∠B=90°,AB=3,BC=4,AD=12,BD=13,求四边形ABCD的面积.