题目内容
20.观察下列各式:①f(1)=$\frac{\sqrt{2}-1}{2}$;②f(2)=$\frac{\sqrt{3}-\sqrt{2}}{2}$;③f(3)=$\frac{\sqrt{4}-\sqrt{3}}{2}$;④f(4)=$\frac{\sqrt{5}-\sqrt{4}}{2}$…
回答下列问题:
(1)利用你观察到的规律求f(n);
(2)计算:(2$\sqrt{2015}$+2)[f(1)+f(2)+f(3)+…+f(2014)].
分析 (1)根据题目所给的式子,可得f(n)=$\frac{\sqrt{n+1}-\sqrt{n}}{2}$;
(2)根据式子规律,将各个数代入,进行化简求解.
解答 解:(1)f(n)=$\frac{\sqrt{n+1}-\sqrt{n}}{2}$;
(2)原式=2($\sqrt{2015}$+1)[$\frac{\sqrt{2}-1}{2}$+$\frac{\sqrt{3}-\sqrt{2}}{2}$+$\frac{\sqrt{4}-\sqrt{3}}{2}$+…+$\frac{\sqrt{2015}-\sqrt{2014}}{2}$]
=($\sqrt{2015}$+1)[$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…$\sqrt{2015}$-$\sqrt{2014}$]
=($\sqrt{2015}+1$)($\sqrt{2015}$-1)
=2015-1
=2014.
点评 本题考查了二次根式的混合运算,解答本题的关键是根据题目找出规律,写出f(n)的代数式.

练习册系列答案
相关题目
 如图,∠AOB=45°,过OA上到点O的距离分别为1的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3….则第一个黑色梯形的面积S1=4;观察图中的规律,第n(n为正整数)个黑色梯形的面积Sn=8n-4.
如图,∠AOB=45°,过OA上到点O的距离分别为1的点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为S1,S2,S3….则第一个黑色梯形的面积S1=4;观察图中的规律,第n(n为正整数)个黑色梯形的面积Sn=8n-4.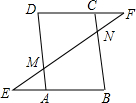 如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.
如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.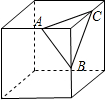 如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )
如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )