题目内容
4.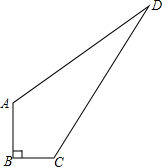 如图,∠B=90°,AB=3,BC=4,AD=12,BD=13,求四边形ABCD的面积.
如图,∠B=90°,AB=3,BC=4,AD=12,BD=13,求四边形ABCD的面积.
分析 连接AC,根据勾股定理求出AC,根据勾股定理的逆定理求出△CAD是直角三角形,分别求出△ABC和△CAD的面积,即可得出答案.
解答 解:连结AC,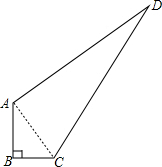
在△ABC中,
∵∠B=90°,AB=4,BC=3,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5,
∴S△ABC=$\frac{1}{2}$×3×4=6
在△ACD中,
∵AD=12,AC=5,CD=13,
∴AD2+AC2=CD2,
∴△ACD是直角三角形,
∴S△ACD=$\frac{1}{2}$×5×12=30.
∴四边形ABCD的面积=S△ABC+S△ACD=6+30=36.
点评 本题考查了勾股定理,勾股定理的逆定理的应用,解此题的关键是能求出△ABC和△CAD的面积,注意:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形是直角三角形.

练习册系列答案
相关题目
13.下列二次根式属于最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{3}$ | C. | $\sqrt{\frac{2}{5}}$ | D. | $\sqrt{1.4}$ |
14.下列式子中,x可以取1和2的是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{x-2}$ | C. | $\frac{2}{x-1}$ | D. | $\frac{2}{x-2}$ |
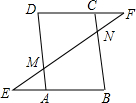 如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.
如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.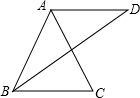 如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.
如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.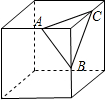 如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )
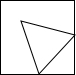
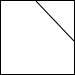
如图,是一个切去了一个角的正方体,切面与棱的交点A,B,C均是棱的中点,得到的几何体的主视图是( )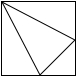

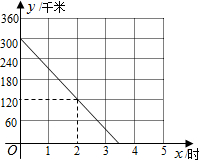 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.