题目内容
7.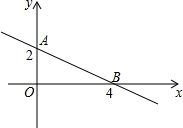 若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求:
若y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数.求:(1)m的值;
(2)函数解析式;
(3)直线与两坐标围成的三角形面积.
分析 (1)根据一次函数的定义解答即可;
(2)把m的值代入解析式中可得一次函数的解析式;
(3)根据解析式解得与坐标轴的交点,即可得出直线与两坐标围成的三角形面积.
解答 解:(1)因为y=(m-2)${x}^{{m}^{2}-2}$+m-1是一次函数,
可得:m-2≠0,且m2-2=1,
解得:m=±$\sqrt{3}$;
(2)把m=±$\sqrt{3}$代入y=(m-2)${x}^{{m}^{2}-2}$+m-1可得:y=($\sqrt{3}$-2)x+$\sqrt{3}$-1或y=(-$\sqrt{3}$-2)x-$\sqrt{3}$-1;
(3)直线y=($\sqrt{3}$-2)x+$\sqrt{3}$-1与两坐标围成的三角形面积=$\frac{1}{2}×(\sqrt{3}-1)×(-\frac{\sqrt{3}-1}{\sqrt{3}-2})=1$;
直线y=(-$\sqrt{3}$-2)x-$\sqrt{3}$-1与两坐标围成的三角形面积=$\frac{1}{2}×(\sqrt{3}+1)×\frac{-\sqrt{3}-1}{-\sqrt{3}-2}=1$.
点评 此题考查一次函数的定义,关键是根据一次函数的定义得出m的值.

练习册系列答案
相关题目
1.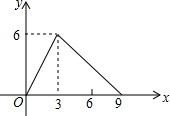 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
 如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )
如图所示是函数y=f(x)的图象,则y=f(f(2))的值为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
17.下列事件为必然事件的是( )
| A. | 任意买一张电影票,座位号是奇数 | |
| B. | 两边及其夹角对应相等的两个三角形全等 | |
| C. | 打开电视机,正在播放纪录片 | |
| D. | 三根长度为4cm,4cm,8cm的木棒能摆成三角形 |
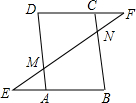 如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.
如图,已知点E、F是?ABCD的边BA、DC的延长线的点,且AE=CF,线段EF分别交AD、BC于点M、N,找出图中所有的全等三角形,并加以证明.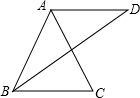 如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.
如图,已知AB=AC=AD,且AD∥BC,试说明∠C与∠D之间的关系.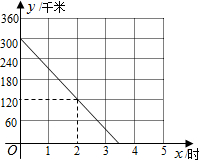 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,甲车在行驶过程中速度始终不变.甲车距B城高速公路入口处的距离y(千米)与行驶时间x(时)之间的关系如图.