题目内容
20.若一元二次方程ax2+bx+c=0的两根分别为1,2.求一元二次方程cx2+ax+b=0的两根.分析 根据了一元二次方程的解的定义得到$\left\{\begin{array}{l}{a+b+c=0}\\{4a+2b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-3a}\\{c=2a}\end{array}\right.$,则一元二次方程cx2+ax+b=0化为2ax2+ax-3a=0,整理得2x2+x-3=0,然后利用因式分解法解此方程即可.
解答 解:∵一元二次方程ax2+bx+c=0的两根分别为1,2,
∴$\left\{\begin{array}{l}{a+b+c=0}\\{4a+2b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-3a}\\{c=2a}\end{array}\right.$,
∴一元二次方程cx2+ax+b=0化为2ax2+ax-3a=0,即2x2+x-3=0,
解得x1=-$\frac{3}{2}$,x2=1,
即一元二次方程cx2+ax+b=0的两根分别为-$\frac{3}{2}$,1.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
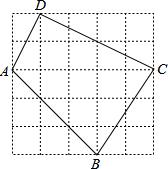 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形.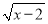 有意义的x的取值范围是( )
有意义的x的取值范围是( )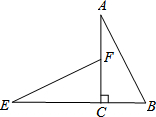 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°得到Rt△EFC.若AB=$\sqrt{5}$,BC=1,则线段BE的长为3,顶点A所运动过的路程等于π(保留π).