题目内容
20.代数式ax2+bx+c在x为1,2,-1时,它的值分别为-6,-11,-8.则a+2b+3c=-15.分析 将对应数值代入得到关于a、b、c的三元一次方程组,然后求得a、b、c的值
解答 解:根据题意得:$\left\{\begin{array}{l}{a+b+c=-6①}\\{4a+2b+c=-11②}\\{a-b+c=-8③}\end{array}\right.$
①-③得:2b=2.
解得:b=1.
①+②得;2a+2c=-14,即a+c=-7④.
将b=1代入②得:4a+c=-13⑤.
⑤-④得:a=-2.
∴c=-5.
将a=-2,b=1,c=-5代入得:a+2b+3c=-2+2×1+3×(-5)=-15.
故答案为:-15.
点评 本题主要考查的是求代数式的值,根据题意列出关于a、b、c的方程组,从而求得a、b、c的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
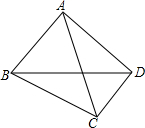 如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD.
如图,四边形ABCD中,∠BAC=∠BCD=90°,若AC平分∠BCD,求证:AB=AD. 看图填空,并在括号内注明说理依据.
看图填空,并在括号内注明说理依据. 如图,假设三角形ABC的面积为1平方分米,且BE=2EC,F是CD的中点.那么,阴影部分的面积是多少分米?
如图,假设三角形ABC的面积为1平方分米,且BE=2EC,F是CD的中点.那么,阴影部分的面积是多少分米?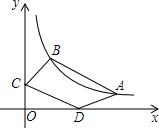 在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求:
在反比例函数y=$\frac{8}{x}$(x>0)的图象上有不重合的A、B两点,A点横坐标为8,B点横坐标为4.求: