Question

5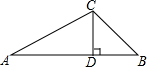．南沙群岛是我国股友领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至A处时，该岛位于正东方向的B处，为了防止某国海巡警干扰，就请求我国C处的渔监船前往B处护航，测得C与AB的距离CD为20海里，已知A位于C处的南偏西60°方向上，B位于C的南偏东45°的方向上，求A、B之间的距离．（$\sqrt{3}$≈1.7，结果精确到1海里）

Answer 1

分析 先解Rt△ACD，求出AD，再解Rt△BCD，求出BD，根据AB=AD+BD代入计算即可．

解答 解：由题意，可知CD=20海里，∠ACD=60°，∠BCD=45°．
在Rt△ACD中，∵∠ACD=60°，CD=20，
∴AD=CD•tan∠ACD=20$\sqrt{3}$．
在Rt△BCD中，∵∠BCD=45°，CD=20，
∴BD=CD•tan∠BCD=20，
∴AB=AD+BD=20$\sqrt{3}$+20≈54（海里）．
答：A、B之间的距离约为54海里．

点评 本题考查了解直角三角形的应用-方向角问题，解答本题的关键是利用三角函数求出AD与BD的长度，难度一般．