题目内容
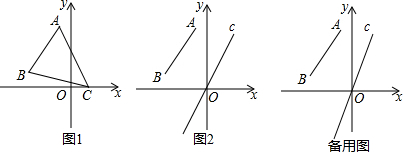
3.如图,在平面直角坐标系中,A(a,4),B(b,1),C(c,0),且(b-a+2)2+$\sqrt{b-3a}$+|c-1|=0.(1)求a,b,c;
(2)若将线段AB,以1个单位/s的速度沿x轴方向向右平移,t秒后平移后的三角形ABO与平移前的三角形ABC的面积相等,求运动时间t;
(3)过原点O的一条直线e上任意一点的坐标P(m,n)都满足n=3m,例如直线e上的点(1,3),(1.5,4.5),(-1,-3),(-2,-6),…,等都满足n=3m,在坐标轴上是否存在一点N,同时在直线e上是否存在一点M,使得四边形ABMN或四边形ABNM构成平行四边形?若存在,求出点N的坐标;若不存在,说明理由.
分析 (1)根据非负数的性质即可解决问题;
(2)切线直线AB的解析式,求出直线AB与x轴的交点M,设t秒后平移后的三角形ABO与平移前的三角形ABC的面积相等,则平移后直线AB的解析式为y=$\frac{3}{2}$(x-t)+$\frac{11}{2}$,与x轴的交点M为(t-$\frac{11}{3}$,0),A(t-1,4),B(t-3,1),$\frac{1}{2}$构建方程即可解决问题;
(3)由题意点M在直线y=3x上,当点M的横坐标为±2或纵坐标为±3时,满足条件,再分别求解即可解决问题;
解答 解:(1)∵(b-a+2)2+$\sqrt{b-3a}$+|c-1|=0,
又∵(b-a+2)2≥0,$\sqrt{b-3a}$≥0,|c-1|≥0,
则有$\left\{\begin{array}{l}{b-a+2=0}\\{b-3a=0}\\{c=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-1}\\{b=-3}\\{c=1}\end{array}\right.$.
(2)如图1中,
∵A(-1,4),B(-3,1),
∴直线AB的解析式为y=$\frac{3}{2}$x+$\frac{11}{2}$,
∴直线与x轴的交点M(-$\frac{11}{3}$,0),
∴S△ABC=S△ACM-S△BCM=$\frac{1}{2}$×$\frac{14}{3}$×4-$\frac{1}{2}$×$\frac{14}{3}$•1=7,
设t秒后平移后的三角形ABO与平移前的三角形ABC的面积相等,
则平移后直线AB的解析式为y=$\frac{3}{2}$(x-t)+$\frac{11}{2}$,与x轴的交点M为(t-$\frac{11}{3}$,0),A(t-1,4),B(t-3,1),
∴$\frac{1}{2}$•(t-$\frac{11}{3}$)•(4-1)=7,
∴t=$\frac{25}{3}$s.
(3)如图2中,
由题意点M在直线y=3x上,当点M的横坐标为±2或纵坐标为±3时,分别得到M1(2,6),M2(1,3),M3(-1.-3),M4(-2,-6),
作M1N1∥AB交y轴于N1,易知N1(0,3),由△ABK≌△M1N1H1,可知AB=M1N1,点N1满足条件,
同法可得N2(-1,0),N3(1,0),N4(0,-3)也满足条件.
点评 本题考查四边形综合题、一次函数的应用、三角形的面积、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会构造全等三角形解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | 55°25′ | B. | 56°25′ | C. | 63°5′ | D. | 56°35′ |
| A. | ±8 | B. | -8 | C. | 8 | D. | ±4 |
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |




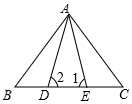 已知如图所示,∠1=∠2,∠B=∠C,BD=CE;写出图中全等的三角形是△ABD≌△ACE;△ABE≌△ACD.
已知如图所示,∠1=∠2,∠B=∠C,BD=CE;写出图中全等的三角形是△ABD≌△ACE;△ABE≌△ACD. 如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.
如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的平分线,BD、CE交于点O.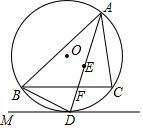 如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.
如图,点E是△ABC的内心,AE的延长线与BC交于点F,与△ABC的外接圆⊙O交于点D,⊙O的切线PD交AB的延长线于点P.