题目内容
9.a、b、c是△ABC的∠A、∠B、∠C的对边,且a:b:c=1:$\sqrt{2}$:$\sqrt{3}$,则cosB的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
分析 根据勾股定理的逆定理可知该三角形为直角三角形,然后再根据余弦函数的定义求解即可.
解答 解:∵${1}^{2}+(\sqrt{2})^{2}=(\sqrt{3})^{2}$,
∴△ABC为直角三角形.
cosB=$\frac{a}{c}$=$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$.
故选C.
点评 本题主要考查的是勾股定理的逆定理和锐角三角函数的定义,得出△ABC为直角三角形是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,四边形ABCD是菱形,CE⊥AD于点E,CF⊥AB于点F.求证:CE=CF.
如图,四边形ABCD是菱形,CE⊥AD于点E,CF⊥AB于点F.求证:CE=CF.



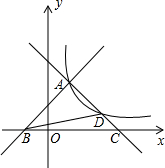 如图,直线y=x+1和y=-x+3相交于点A,且分别与x轴交于B,C两点,过点A的双曲线y=$\frac{k}{x}$(x>0)与直线y=-x+3的另一交点为点D.
如图,直线y=x+1和y=-x+3相交于点A,且分别与x轴交于B,C两点,过点A的双曲线y=$\frac{k}{x}$(x>0)与直线y=-x+3的另一交点为点D.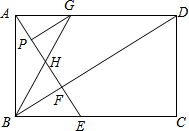 如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论:
如图,在矩形ABCD中,AE⊥BD交BC于E,垂足为F,BG平分∠ABD交AE于H,GP∥BD交AE于P,下列结论: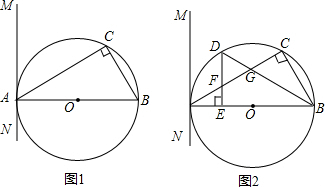
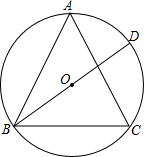 等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.
等边三角形ABC的顶点都在圆O上,BD为直径,则∠BDC=60°,∠ACD=30°,若CD=6cm,则△ABC的面积等于27$\sqrt{3}$cm2.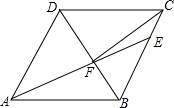 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC,BD于点E,F,CE=2,连接CF,以下结论::①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③CF=5;④△CEF的面积为$\frac{6}{5}$$\sqrt{3}$.其中一定成立的是①②④(把所有正确结论的序号都填在横线上).