题目内容
9．
如图，四边形ABCD是菱形，CE⊥AD于点E，CF⊥AB于点F．求证：CE=CF．
分析 连接AC，根据菱形的性质可得AC平分∠DAE，再根据角平分线的性质可得CE=FC．
解答 
证明：连接AC，
∵四边形ABCD是菱形，
∴AC平分∠DAE，
∵CE⊥AB，CF⊥AD，
∴CE=FC．
点评 此题主要考查了菱形的性质，以及角平分线的性质，关键是掌握菱形的两条对角线互相垂直，并且每一条对角线平分一组对角；角平分线的性质：角的平分线上的点到角的两边的距离相等．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
19．小军家距学校3千米，原来他骑自行车上学，学校为保阵学生安全，新购进校车接送学生．若校车速度是他骑车速度的2倍，现在小军乘校车上学可以从家晚20分钟出发，结果与原来到校时间相同．设小军骑车的速度为x千米/小时，则所列方程正确的为（ ）
| A． | $\frac{3}{x}$+$\frac{1}{3}$=$\frac{3}{2x}$ | B． | $\frac{3}{x}$+20=$\frac{3}{2x}$ | C． | $\frac{3}{x}$-$\frac{1}{3}$=$\frac{3}{2x}$ | D． | $\frac{3}{x}$-20=$\frac{3}{2x}$ |
如图，∠1与∠2是直线AB和直线CE被第三条直线BD所截得的同位角．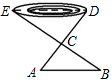
如图，为了测量一个池塘的宽DE，在岸边找一个点C，测得CD=15m，在DC的延长线上找一点A，使AC=10m，过A作AB∥DE交EC的延长线于点B，测得AB=16m，求池塘的宽DE．
9．a、b、c是△ABC的∠A、∠B、∠C的对边，且a：b：c=1：$\sqrt{2}$：$\sqrt{3}$，则cosB的值是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |