题目内容
7.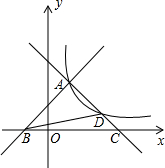 如图,直线y=x+1和y=-x+3相交于点A,且分别与x轴交于B,C两点,过点A的双曲线y=$\frac{k}{x}$(x>0)与直线y=-x+3的另一交点为点D.
如图,直线y=x+1和y=-x+3相交于点A,且分别与x轴交于B,C两点,过点A的双曲线y=$\frac{k}{x}$(x>0)与直线y=-x+3的另一交点为点D.(1)求双曲线的解析式;
(2)求△BCD的面积.
分析 (1)先通过解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-x+3}\end{array}\right.$得A(1,2),然后把A(1,2)代入y=$\frac{k}{x}$中求出k的值即可得到反比例函数解析式;
(2)根据反比例函数与一次函数的交点问题,通过解方程组$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=-x+3}\end{array}\right.$得D(2,1),再利用x轴上点的坐标特征确定B点和C点坐标,然后根据三角形面积公式求解即可.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
则A(1,2),
把A(1,2)代入y=$\frac{k}{x}$得k=1×2=2,
所以反比例函数解析式为y=$\frac{2}{x}$;
(2)解方程组$\left\{\begin{array}{l}{y=\frac{2}{x}}\\{y=-x+3}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
则D(2,1),
当y=0时,x+1=0,解得x=-1,则B(-1,0);
当y=0时,-x+3=0,解得x=3,则C(3,0),
所以△BCD的面积=$\frac{1}{2}$×(3+1)×1=2.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 抽取的10台电视机 | B. | 这一批电视机的使用寿命 | ||
| C. | 10 | D. | 抽取的10台电视机的使用寿命 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
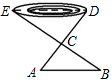 如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.
如图,为了测量一个池塘的宽DE,在岸边找一个点C,测得CD=15m,在DC的延长线上找一点A,使AC=10m,过A作AB∥DE交EC的延长线于点B,测得AB=16m,求池塘的宽DE.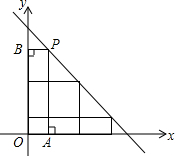 如图,在一次函数y=-x+6的图象上取一点P,作PA⊥x轴于点A,PB⊥y轴于点B,且矩形PBOA的面积为5,则在x轴的上方满足上述条件的点P的个数共有( )
如图,在一次函数y=-x+6的图象上取一点P,作PA⊥x轴于点A,PB⊥y轴于点B,且矩形PBOA的面积为5,则在x轴的上方满足上述条件的点P的个数共有( )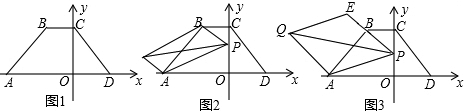
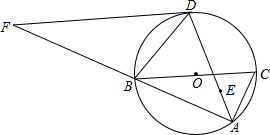 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F.
如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆⊙O相交于点D,BC是⊙O的直径,⊙O的切线FD与AB的延长线交于点F. 如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.
如图,在△ABC中,∠ABC=100°,∠ACB的平分线交AB边于E,在AC边上有一点D满足∠CBD=20°,连结DE,求∠CED的度数.