题目内容
16. 在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).
在平面直角坐标系中,△ABC的位置如图所示,三个顶点的坐标分别为:A(1,2)、B(2,3)、C(3,0).(1)现将△ABC先向左平移5个单位长度,再向上平移2个单位长度,得到△A1B1C1,请在平面直角坐标系中画出△A1B1C1.
(2)此时平移的距离是$\sqrt{29}$;
(3)在平面直角坐标系中画出△ABC关于点O成中心对称的△A2B2C2.
分析 (1)利用点平移的坐标规律写出点A、B、C平移后的对应点A1、B1、C1,然后描点即可得到△A1B1C1.
(2)利用勾股定理计算;
(3)利用关于原点对称的点的坐标特征写出点A、B、C的对应点A2、B2、C2,然后描点即可得到△A2B2C2.
解答 解:(1)如图,△A1B1C1为所作;
(2)此时平移的距离=$\sqrt{{5}^{2}+{2}^{2}}$=$\sqrt{29}$;
故答案为$\sqrt{29}$;
(3)如图,△A2B2C2为所作.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.

练习册系列答案
相关题目
5.如果点A(a,b)在第二象限,则点B(b,a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求:
平行四边形ABCD在平面直角坐标系中的位置如图所示,已知AB=8,AD=6,∠BAD=60°,点A的坐标为(-2,0).求: 如图,长方形ABCD中,AB=5cm,AD=9cm,现将该长方形沿BC方向平移,得到长方形A1B1C1D1,若重叠部分A1B1CD的面积为20cm2,则长方形ABCD向右平移的距离为5cm.
如图,长方形ABCD中,AB=5cm,AD=9cm,现将该长方形沿BC方向平移,得到长方形A1B1C1D1,若重叠部分A1B1CD的面积为20cm2,则长方形ABCD向右平移的距离为5cm. 小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
小明一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶若干小时后,途中在加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题: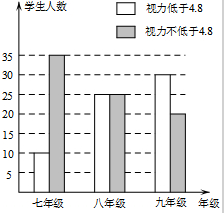 在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题: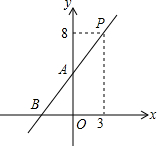 已知:如图,直线y=kx+4(k≠0)经过点A,B,P.
已知:如图,直线y=kx+4(k≠0)经过点A,B,P.