题目内容
11.一组数据:$-\frac{1}{4}$,$\frac{2}{8}$,$-\frac{3}{16}$,$\frac{4}{32}$,$-\frac{5}{64}$中第7个数是-$\frac{7}{256}$,用代数式表示第n个数是(-1)n×$\frac{n}{{2}^{n+1}}$.分析 根据数列规律得出第n个数为(-1)n×$\frac{n}{{2}^{n+1}}$即可得.
解答 解:∵第1个数-$\frac{1}{4}$=(-1)1×$\frac{1}{{2}^{2}}$,
第2个数$\frac{2}{8}$=(-1)2×$\frac{2}{{2}^{3}}$,
第3个数-$\frac{3}{16}$=(-1)3×$\frac{3}{{2}^{4}}$,
…
∴第7个数为(-1)7×$\frac{7}{{2}^{8}}$=-$\frac{7}{256}$,
第n个数为(-1)n×$\frac{n}{{2}^{n+1}}$,
故答案为:-$\frac{7}{256}$,(-1)n×$\frac{n}{{2}^{n+1}}$.
点评 本题主要考查数字的变化规律,根据数列的变化规律得出第n个数为(-1)n×$\frac{n}{{2}^{n+1}}$是解题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1.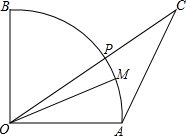 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
 如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )
如图,扇形OAB半径OA=2,M为$\widehat{AB}$上一点,∠AOM=30°,点P为$\widehat{BM}$上一动点,C为OP延长线上一点,且∠ACO=30°,当点P运动时,设线段AC的最大值为a,最小值为b,则a-b的值为( )| A. | 4 | B. | 2 | C. | 2-$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
2. 二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
(1)确定二次函数y1与直线AB的解析式y2;
(2)根据图象,分别确定当y1<y2,y1=y2时,自变量x的取值范围.
 二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.
二次函数y1=a(x-2)2的图象与直线交于A(0,-1),B(2,0)两点.(1)确定二次函数y1与直线AB的解析式y2;
(2)根据图象,分别确定当y1<y2,y1=y2时,自变量x的取值范围.
20. 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
表1 阅读课外书籍人数分组统计表
请你根据以上信息解答下列问题:
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.
某校为了了解该校初二年级学生阅读课外书籍的情况,随机抽取了该年级的部分学生,对他们某月阅读课外书籍的情况进行了调查,并根据调查的结果绘制了如图的统计图表.表1 阅读课外书籍人数分组统计表
| 分组 | 阅读课外书籍时间n(小时) | 人数 |
| A | 0≤n<3 | 3 |
| B | 3≤n<6 | 10 |
| C | 6≤n<9 | a |
| D | 9≤n<12 | 13 |
| E | 12≤n<15 | b |
| F | 15≤n<18 | c |
(1)这次共调查了学生多少人?
(2)E组人数在这次调查中所占的百分比是多少?
(3)求出表1中a的值,并补全图1;
(4)若该年级共有学生300人,请你估计该年级在这月里阅读课外书籍的时间不少于12小时的学生约有多少人?
 如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.
如图是一座抛物形拱桥,当水面的宽为12m时,拱顶离水面4m,当水面下降3m时,水面的宽为6$\sqrt{7}$m.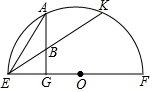 如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.
如图,A是以EF为直径的半圆上的一点,作AG⊥EF交EF于G,又B为AG上一点,EB的延长线交半圆于点K,若EB=2,EK=6,则AE=2$\sqrt{3}$.