题目内容
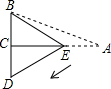如图，在三角形纸片ABC中，∠BCA=90°，∠BAC=30°，AC=3| 3 |
| A、2 | ||
| B、3 | ||
C、2
| ||
D、
|
考点：翻折变换（折叠问题）
专题：
分析：在Rt△ABC中求出AB=6，BC=3，根据折叠的性质可得BD=BA=6，∠D=∠A=30°，在Rt△DCE中可求出DE．
解答：解：在Rt△ABC中，∵∠BAC=30°，AC=3
，
∴AB=6，BC=3，
由折叠的性质可得：BD=BA=6，∠D=∠A=30°，
∴CD=BD-BC=3，
∴DE=
=
=2
．
故选C．
| 3 |
∴AB=6，BC=3，
由折叠的性质可得：BD=BA=6，∠D=∠A=30°，
∴CD=BD-BC=3，
∴DE=
| CD |
| cos∠D |
| 3 | ||||
|
| 3 |
故选C．
点评：本题考查了翻折变换及解直角三角形的知识，注意掌握翻折前后对应边相等、对应角相等，难度一般．
练习册系列答案
相关题目
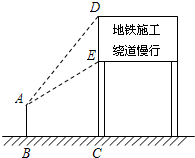某市地铁工程正在加快建设，为了缓解市区内一些主要路段交通拥挤的现状，交警大队在一些主要路口设立了交通路况指示牌，如图所示，小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和32°．求路况指示牌DE的高度．（精确到0.01米）
如图，在矩形ABCD中，点M、N在线段AD上，∠MBC=∠NCB=60°，点E、F分别为线段CN、BC上的点，连接EF并延长，交MB的延长线于点G，EF=FG．
在△ABC中，∠A是钝角，H是垂心，AH=BC，则∠BHC=（ ）
| A、30° | B、45° |
| C、60° | D、75° |
如图，在Rt△ABC中，∠ABC=90°，BA=BC．点D是AB的中点，连接CD，过点B作BG丄CD，分别交CD、CA于点E、F，与过点A且垂直于AB的直线相交于点G，连接DF．给出以下四个结论：①
商城义乌江的两岸绿树葱茏、生机勃勃，成为我市一道亮丽的风景．如图，从义乌江的南岸C点测得两处风景A、B两点的视角∠ECA和∠ACB分别为30°和105°，测得BC=100